4.2.3. Magnetic fields versus Gas density, on large linear scales (B ~ n0.2)
Early results with limited data gave inconclusive relationships, spanning the whole range of exponent k, from k = 0 to k = 2/3. At low gas density, early observations were plagued by lack of data. Troland and Heiles (1986) and Heiles (1987) proposed that B ~ n0 at low gas density n < 100 cm-3, since gas density increases can occur through quiescent streaming of thermal gas going along magnetic field lines, without the need to increase the B strength. Models by Bertoldi and McKee (1992) suggested that non-self-gravitating clumps in a cloud were supported by the internal pressure of the cloud, so that there is no mass-dependent force to enhance the magnetic field, leading to B ~ n0. Fleck (1988, his Equ. 24) also modeled a low density non-self-gravitating cloud with B ~ n0. Kronberg (1994) proposed that since intergalactic magnetic field energy densities are close to the energy density of the Cosmic Microwave Background Radiation (CMBR = 2.7° K), this implied a CMBR-equivalent magnetic field strength of 3 µGauss which can be viewed as a saturation limit in absence of stronger amplification processes, i.e., B ~ n0. Myers (1990) noted that the emitted line width from non-self-gravitating clouds at low gas density values was comparable to the Alfven speed and was almost constant, and he predicted that B ~ n0.5 with a model having a strong magnetic field.
Caveat. At low gas density n = 5 cm-3, an
observational claim of a B ~ n0.65 law in the
galaxy M31 has been reported, where B values have
been measured from one type i of objects
(interstellar synchrotron electrons, scales of 1 kpc) located
outside molecular clouds, and
where the corresponding gas density values n were measured from
another type j of objects
(atomic and molecular gas, cloud scales of 1 pc) located inside
molecular clouds (e.g.,
Berkhuijsen et al. 1993,
their Fig. 11, with B from intercloud
synchrotron electrons and n
from CO molecular lines). As these are different objects,
i 
j,
this data selection invalidates claims that
Bi ~ nik for M31, since
both B OUTSIDE clouds and n OUTSIDE clouds
should be used, and not B OUTSIDE with gas density n INSIDE
extrapolated to predict n OUTSIDE.
Since then, better and more numerous data allowed more conclusive relations.
B ~ n0.2 . With the availability of many more observations, better statistics have now come out. For each object, care must be taken that one measures the gas density n and the magnetic field B from the same object - i.e., a B value should not come from a different object than the object used to measure the gas density n value. At low gas density n < 100 cm-3 , the first detection of a non-zero relationship between the gas density n and the magnetic field B on cosmic scales (> 100 pc ) was found by Vallée (1990b - see his Fig. 4), indicating a law of the form B ~ nk , where the exponent k = 0.2 ± 0.05. This indicated the prevalence of some types of turbulence on large scales.
More data became available, with which Vallée (1995d) since confirmed this trend with B ~ n0.2.
Figure 13, from Vallée (1995d), shows a B ~ nk law, with an exponential value k = 0.17 ± 0.03 for gas density values n < 100 cm-3 on cosmic scales (> 100 pc). Thus the k value is non-zero at the 5 rms level.
 |
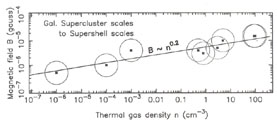Figure 13. Observed behavior of the
magnetic field B (in gauss) with the gas density
n (in cm-3), for objects with n < 100
cm-3. The least-squares fitted line has
B |
Theoretically, intermediate relations have been predicted. B ~ n1/4 was used in the model of Henriksen (1991) with regions of little cooling and no shock, B ~ n1/3 was used in the incompressible turbulence models (e.g., Myers 1983), as well as in MHD turbulent models (e.g., Pellegatti-Franco et al. 1985).
6 µGauss
(n / cm-3)0.2. A possible
interpretation involves the free motion of matter along the
magnetic field lines, accreting slowly at some points with little
increase in B strength. See