


2.3. Magnetic Moment and Angular Momentum
The angular momentum A of a spherical object of radius rsurf is
 |
where  =
2
=
2 (rotation
period)-1 , and mass is the mass of the object. Thus for the
Sun (
(rotation
period)-1 , and mass is the mass of the object. Thus for the
Sun ( = 2.9 ×
10-6 sec-1) one gets
A
= 2.9 ×
10-6 sec-1) one gets
A  1042
kg m2 sec-1; the Sun's magnetic moment
Msurf
1042
kg m2 sec-1; the Sun's magnetic moment
Msurf
 3 ×
1027 Gauss m3 . For Mercury
(
3 ×
1027 Gauss m3 . For Mercury
( = 1.2 ×
10-6 sec-1),
A
= 1.2 ×
10-6 sec-1),
A  1030 kg m2 sec-1, and
Msurf
1030 kg m2 sec-1, and
Msurf
 5 ×
1016 Gauss m3.
5 ×
1016 Gauss m3.
A direct relationship is often but not always observed between the magnetic dipole moment Msurf of an object and its angular momentum A. This often observed relation is given approximately by
 |
Figure 4 shows this equation (dashed), along with the observational data. Originally proposed only for the planets, this empirical law has been extended to include the Sun (e.g., Blackett 1947; Russell 1978), and big moons such as Ganymede and Io (Kivelson et al. 1996a, 1996b).
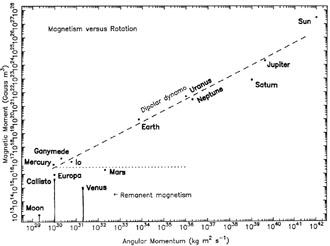 |
Figure 4. Observed relation between the
magnetic moment and the angular momentum of
moons, planets, and the Sun. The dashed line follows the equation for a
dipolar dynamo, with a slope of
|
Such a law has been called a "magnetic Bode's law" (Russell 1978), and was though to be a "long-sought connection between electromagnetic and gravitational phenomena" (Blackett 1947), and has also been called "an effect more along 'meteorological' lines" (e.g., chapter 18 in Parker 1979).
This relationship may now be better called a "dipolar dynamo law", for
three reasons.
(1) All the moons, planets and star(s) that obey so far this relation
do have a dipolar
dynamo. (2) All the moons and planets without a significant magnetic
dynamo (Earth's
Moon, Venus, Mars) do not follow this law - the observed data for
Earth's Moon, Venus, and
Mars fall significantly below the Msurf values
predicted by this law (e.g.,
Kivelson et al. 1996b).
(3) The relationship may not work for other (not dypolar) dynamo types
- thus our Milky
Way galaxy has a planar disk with an axisymmetric spiral (not dipolar)
dynamo magnetic field, with
A  3 ×
1067 kg m2 sec-1 and
Msurf
3 ×
1067 kg m2 sec-1 and
Msurf
 9 ×
1055 Gauss m3, and thus the equation above
would predict only Msurf
9 ×
1055 Gauss m3, and thus the equation above
would predict only Msurf
 4 ×
1047 Gauss m3 -
about 108 times lower than observed.
4 ×
1047 Gauss m3 -
about 108 times lower than observed.
Physically, no direct physical justification for this law has been found. Mathematically, since Msurf = Bsurf . r3surf for a sphere, and since A ~ (mass) . r2surf ~ (density) . r5surf then it can be seen that Msurf and A are strong powers of rsurf, so the apparent correlation of these two quantities should predict Msurf ~ r3surf ~ A0.60 . This mathematical argument would predict that the data for all planets would follow this law - this argument does not explain why the observed data for some planets or some moons fall below the predictions of this law.