


3.3. Normal Stars (~ 106 to 107 km; ~ 10-7 pc)
In normal stars, dynamos can explain the basics of a stellar magnetic field, as long as a convective envelope exists in the stellar interior. But theoreticians have yet to arrive at an adequate, complete, self-consistent MHD dynamo model of a convective envelope that can reproduce quantitatively all relevant observations at the same time (e.g., Donati et al. 1997).
3.3.1. Dipolar Magnetic Field Shape
The internal structure of a star is reasonably well understood. The energy released in the interior of stars and in the assemblages of stars by the action of nuclear and gravitational forces keeps electrically conducting fluids in turbulent motion. Magnetic field in cool stars originate from the base of the outer convection zone and migrate towards the stellar surface through magnetic buoyancy. The magnetic field entrained in the fluid (ionized gas) is stretched and folded by the fluid motion (nonuniform rotation and cyclonic convection), gaining energy in the process (e.g., Parker 1983). Main sequence stars rotate and have vigorous convective zones (like the Sun), so it follows that there is a dynamo effect in these stars. The younger stars would seethe with activity, but their magnetic virility would decline over a period of 108 years (e.g., chapter 21 in Parker 1979).
An important mechanism to detect stellar magnetic fields at optical wavelenths is the Zeeman effect, where emitted lines from chemical elements (e.g., sodium) placed in a magnetic field are splitted into components and the state of splitting depends on the direction and strength of the magnetic field. The application of the Zeeman effect to the optical spectra of certain other classes of star has shown that some stars do possess magnetic fields. Different absorption lines can be used for the Zeeman effect, depending on the star's surfae temperature and hence on the star's spectral type (from hot O-type and B-type stars, normal A-type, F-type, and G-type stars, to cool K-type and M-type stars).
There is typically one large scale dipole and many small localized surface scale dipoles. Stellar-type magnetic fields often have a basic large scale dipolar shape near the stellar surface.
Rapidly rotating active stars generally display stellar spots near their two poles, which is a way to prevent dynamo saturation at high rotation rate (e.g., Solanski et al. 1997). A dynamo could start saturating when rotation is too high, due to the back reaction of the magnetic field on the stellar convection and differential rotation. Slower rotators like the G-type Sun tend to have their spots near the equatorial plane. The magnetic flux tubes are rising from deep inside the star, due mainly to magnetic buoyancy and Coriolis force, and secondarily to magnetic tension and drag.
A detection of a magnetic field in a supposedly 100% convective star or in a 100% radiative star could be challenging for dynamo theories. Some low-mass pre-main-sequence objets (such as V410 Tau) are claimed to have no inner radiative zone, being 100% convective stars, yet they may have a detectable magnetic field. Some high-mass pre-main-sequence objects (such as HD 104237) are claimed to have no convective envelope, being 100% radiative stars, yet they may have a magnetic field - in such cases, the theoretical work is being concentrate on the possible presence of a small sub-photospheric layer with turbulent motions (e.g., Donati et al. 1997).
Many stars in a sub-class of spectral type A stars, called peculiar A stars or Ap stars, have strong surface magnetic fields. The magnetic dipole axis are often perpendicular or oblique with respect to the star's rotation axis, causing a periodic change in the Zeeman line data.
Thus in an ideal case the "effective" magnetic field B, or "longitudinal" magnetic field, or the "line-intensity weighted average over the visible stellar hemisphere of the line-of-sight component of the magnetic vector", is obtained from Stokes V observations and should vary with time t during the rotation period p as
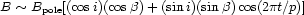 |
where Bpole is the polar magnetic field, i is
the angle between the axis of the magnetic field
dipole and the axis of rotation of the star, and
 is the angle
between our line of sight and
the axis of rotation of the star. The observed separation between the
two Zeeman line
components is proportional to the strength of the magnetic field, ie
is the angle
between our line of sight and
the axis of rotation of the star. The observed separation between the
two Zeeman line
components is proportional to the strength of the magnetic field, ie

 ~
~
 0
ge <B>
where
0
ge <B>
where  0 is
the normalization wavelength and ge is
the average effective Landé factor
(~ 1, within a factor 2). Current observed effective magnetic field
strengths are ~ 10000 Gauss.
0 is
the normalization wavelength and ge is
the average effective Landé factor
(~ 1, within a factor 2). Current observed effective magnetic field
strengths are ~ 10000 Gauss.
Also in the ideal case the "surface" magnetic field, or the "mean field
modulus", or
the "line-intensity weighted average over the visible stellar hemisphere
of the modulus of
the magnetic vector", is obtained from Stokes I observations at
sufficiently high spectral
dispersion showing the spectral lines splitted into several magnetic
components. The
observed line separation between red and blue components for the Zeeman
doublet of the Fe II line at
 6149.258 Åis
given as
6149.258 Åis
given as 
 ~
~
 02
g <B> where
02
g <B> where
 0 is the
normalization wavelength
and g is the Landé factor of the split level
0 is the
normalization wavelength
and g is the Landé factor of the split level
 2.7 here (e.g.,
Mathys et al. 1997).
Current observed surface magnetic field strengths are ~ 3 kG to 10 kG.
2.7 here (e.g.,
Mathys et al. 1997).
Current observed surface magnetic field strengths are ~ 3 kG to 10 kG.
The simultaneous consideration of both the "effective" field and of the "surface" field is required to derive meaningful constraints on the geometrical structure of the magnetic field. Such considerations suggest the following: the magnetic field covers most of the stellar surface, and the two poles within a star often have different strengths, so one magnetic pole could be nearer the stellar surface than the other magnetic pole (e.g., Mathys et al. 1997).
The stellar envelope of Ap stars is hot and radiative, and the magnetic field is thought to be "fossil" - a remainder of the magnetic flux previously in the interstellar medium from which the star formed (e.g., Babel and North 1997).
Some stars have a bow shock. Some X-ray emitting gas around peculiar Ap stars may be due to a shock near such a star, The dipolar magnetic field of 1000 Gauss is able to bend the 500 km/s stellar wind towards the magnetic equatorial disk extending out to 4 stellar radii, resulting in shocked gas near 106 K (Babel & Montmerle 1997).
Calcium emission lines from stellar spots, where the magnetic field is strong, will follow a time variation due to the stellar spot cycle. Since many sun-like, G-type stars show such calcium line variation over time, it has been inferred that about half of the stars similar to the Sun may have magnetic fields.
M-type stars, with a smaller mass than the G-type Sun, are rotating faster than the Sun. All M stars in the Pleiades are rapid rotators (e.g., Jones et al. 1996). They are thus expected to have (i) a predominently polar magnetic field and (ii) temporal magnetic activity possibly concentrated near the stellar poles. Essentially all M stars should display polar, rather than equatorial, temporal magnetic activity. A physical result is that stellar spin-down should be negligible for M stars (e.g., Buzasi 1997)
3.3.4. Stars with a Residual Disk
A small number of stars may have a circumstellar disk (not planets) around, even a long time after star formation. The gas in the circumstellar disk of diameter 0.7 AU around the Be star SS2883 has been modeled with a gas density of 1010 cm-3 and a radial/toroidal magnetic field of 30 Gauss (thin disk) and with a gas density of 108 cm-3 and a poloidal magnetic field of 14 kiloGauss (thick disk), as inferred from the modulation of the RM and DM of the distant orbiting pulsar PSR B1259-63 (e.g., Melatos et al. 1995).
3.3.5. Quadrupolar Magnetic Field Shape
A very small number of stars (< 10) are known to have a global quadrupolar type magnetic field, much like that resulting from two antiparallel dipoles slightly displaced from each other.
This is the case for the B-type star HD37776 with a diameter ~ 8 × 106 km and a magnetic field reaching 2000 Gauss (e.g., Thompson & Landstreet 1985; Borra & Landstreet 1978). This is also the case for the Bp star HD133880, whose very non-sinusoidal magnetic field curve indicates a non-dipolar field geometry, but rather a predominently quadrupolar magnetic field shape with a strength ~ 10000 Gauss (Landstreet, 1990). The Ap star HD137509 has recently been found to exhibit such a quadrupolar magnetic shape with a strength ~ 25000 Gauss (Mathys & Hubrig 1997).
Clearly any mass loss, atmospheric parameter, diffusion velocity, and other quantity that depends on magnetic field strength and shape will be affected by this system of quadruple poles. This is even more so if the magnetic field strength is weak (say 3000 Gauss) at 2 opposite poles and strong (say 10000 Gauss) at the other 2 opposite poles.
Donati & Cameron
(1997)
proposed a novel method to analyse Stokes V data, requiring
a single spectral line fit to over 1500 spectral lines from
 0.470 µm to
0.470 µm to
 0.710 µm,
assuming
all 1500 line shapes/profiles to be additive, self-similar, and scalable
in width and depth. These and other assumptions (weak magnetic field so
that Zeeman splitting is small
compared to the intrinsic line width; limb darkening is constant with
wavelength) sound rough and should be investigated later. Studying the
rapidly rotating (0.5 day) KO dwarf star AB Dor with this novel method,
Donati & Cameron
(1997)
found (i) 6 active magnetic loops with
B ~ 500 Gauss located at high latitudes on the stellar surface
and corona, and (ii) several
other low-latitude spots. Further analysing their data, they deduced
(iii) some clues for a possible surface toroidal magnetic field at high
latitudes going in opposite direction to the
surface toroidal field at intermediate latitudes, predicting (iv)
another two zones of opposite magnetic polarity in the other stellar
hemisphere; hence they theorized (v) a large scale poloidal magnetic
structure ("octupole") inside the star, giving rise to the four surface
toroidal magnetic structure through the interaction with differential
rotation.
0.710 µm,
assuming
all 1500 line shapes/profiles to be additive, self-similar, and scalable
in width and depth. These and other assumptions (weak magnetic field so
that Zeeman splitting is small
compared to the intrinsic line width; limb darkening is constant with
wavelength) sound rough and should be investigated later. Studying the
rapidly rotating (0.5 day) KO dwarf star AB Dor with this novel method,
Donati & Cameron
(1997)
found (i) 6 active magnetic loops with
B ~ 500 Gauss located at high latitudes on the stellar surface
and corona, and (ii) several
other low-latitude spots. Further analysing their data, they deduced
(iii) some clues for a possible surface toroidal magnetic field at high
latitudes going in opposite direction to the
surface toroidal field at intermediate latitudes, predicting (iv)
another two zones of opposite magnetic polarity in the other stellar
hemisphere; hence they theorized (v) a large scale poloidal magnetic
structure ("octupole") inside the star, giving rise to the four surface
toroidal magnetic structure through the interaction with differential
rotation.