


3.5. Neutron Stars (~ 10 km)
When immersed in a strong magnetic field
B  1012
Gauss, the atom
takes a cigar-shaped structure, since the Coulomb force becomes more
effective for binding electrons in the direction parallel to the
magnetic field axis while the electrons are extremely confined in
the direction transverse to the magnetic field axis. Using the atomic
unit a0 = 0.5 × 10-10 m, one finds
that the mean transverse
separation of the electron and proton in the hydrogen atom is
L ~ [2m + 1]0.5 / [426
B12]0.5 atomic units, where
m = 0, 1, 2, 3, ..., and where B12 is the
magnetic field in units of 1012 Gauss. The ionization energy
of the atom becomes EH = 161 eV
for B12 = 1 and rises as
EH
1012
Gauss, the atom
takes a cigar-shaped structure, since the Coulomb force becomes more
effective for binding electrons in the direction parallel to the
magnetic field axis while the electrons are extremely confined in
the direction transverse to the magnetic field axis. Using the atomic
unit a0 = 0.5 × 10-10 m, one finds
that the mean transverse
separation of the electron and proton in the hydrogen atom is
L ~ [2m + 1]0.5 / [426
B12]0.5 atomic units, where
m = 0, 1, 2, 3, ..., and where B12 is the
magnetic field in units of 1012 Gauss. The ionization energy
of the atom becomes EH = 161 eV
for B12 = 1 and rises as
EH  161 [ln(426B12) / ln(426)]2 eV (e.g.,
Lai & Salpeter 1997).
161 [ln(426B12) / ln(426)]2 eV (e.g.,
Lai & Salpeter 1997).
3.5.1. Normal Pulsars (~ 1012 Gauss)
When a normal star with radius R ~ 106 km collapses to form a rotating neutron star or pulsar with radius ~ 10 km, the magnetic flux B will be conserved (B ~ R-2) and the surface magnetic field will increase from ~ 100 Gauss to ~ 1012 Gauss. A previously dipolar shaped magnetic field will remain dipolar shaped. The magnetic field shape of pulsars is generally dipolar, and a magnetosphere is created around the pulsar (e.g., Radhakrishnan & Cooke 1969; Navarro et al. 1997). Neutron stars typically have a gas density decreasing from 1042 cm-3 at the center to 1012 cm-3 at the surface.
The data for normal pulsars are consistent with some kind of passive frozen-in magnetic dipole, of strength ~ 1024 Gauss m3. The radius of a normal pulsar is ~ 10 km, with a mass ~ 1 solar mass, and a rotation period ~ 0.1 sec, giving an angular momentum ~ 5 × 1039 kg. m2 s-1 (not far from the dipolar dynamo law for other bodies).
The basic radio emission process is essentially the same in millisecond-period pulsars and in slower pulsars. The nearby ~ 100 pc PSR J0437-4715 pulsar has a 5.8 millisecond period, a characteristic age of 2.5 × 1010 years, and a dipole magnetic field of 2 × 108 Gauss. This pulsar shows evidence of inertial dragging of its magnetic field lines in the outer magnetosphere, with the low frequency radio emission coming from higher altitudes in the pulsar magnetosphere (e.g., Navarro et al. 1997).
In recent models, the pulsar magnetosphere is divided into closed magnetic field lines (where particles are trapped for long periods of time) and open magnetic field lines (where particles are not confined and are eventually lost to the interstellar medium). In addition, recent models have added a secondary magnetospheric shell, having 1% of the number of particles in the primary shell (e.g., Fig. 4 in Eastlund et al. 1997).
The time evolution of the magnetic field with time in a pulsar is still controversial, a major issue in compact object astrophysics. While some theories favor no magnetic field decay over a long time (e.g., Romani 1990), most theories favor a magnetic field decay of some sort (e.g., Wang 1997). In the decay theories, the pulsar's evolution is divided into three phases: (i) the dipole phase, in which the pulsar spins down through magnetic dipole radiation, ending when the ambient material's ram pressure overcomes the pulsar's wind pressure; (ii) the propeller phase, in which ambient material fills the corotating magnetosphere in a shell above the Alfvénic radius, ending when the shrinking Alfvénic radius becomes smaller than the corotation radius; (iii) the accretion phase, in which the matter accretes directly on the polar cap of the neutron star. In the first (dipolar) and second (propeller) phases, the magnetic field decays either as a law
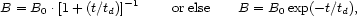 |
with
td  108 years, and B0
108 years, and B0
 1012 Gauss. In
the third (accretion) phase, there is no magnetic
field decay and the field strength remains steady. The 8.4-second pulsar
RX J0720.4-3125
may be in the third or accretion phase (e.g., fig. 1 in
Wang 1997).
1012 Gauss. In
the third (accretion) phase, there is no magnetic
field decay and the field strength remains steady. The 8.4-second pulsar
RX J0720.4-3125
may be in the third or accretion phase (e.g., fig. 1 in
Wang 1997).
Mukherjee & Kembhavi (1997) used statistics to obtain a lower limit on the decay timescale of pulsar magnetic fields (> 160 millions years).
The distance to a pulsar is best determined when one uses a detailed
model of the distribution of free electrons in the disk of the Galaxy.
Taylor & Cordes
(1993)
have provided such a distribution model, with electron density
enhancements in four spiral arms and near the Gum nebula (their equ. 11
and Fig. 1, using a value of 8.5 kpc for the Sun-Galactic
Center distance). From the electron density distribution, one can
compute the plasma frequency and the group velocity at which a radio
signal at a frequency  can
propagate in the interstellar
medium. Comparing time arrivals at two or more frequencies, yields the
dispersion measure DM, an integral of the free electron density over the
distance to the pulsar. Thus the observed DM and the use of the
distribution model for the free electrons will yield the pulsar
distance, to an accuracy of 25%.
can
propagate in the interstellar
medium. Comparing time arrivals at two or more frequencies, yields the
dispersion measure DM, an integral of the free electron density over the
distance to the pulsar. Thus the observed DM and the use of the
distribution model for the free electrons will yield the pulsar
distance, to an accuracy of 25%.
3.5.2. Magnetars (~ 1015 Gauss)
Extreme pulsars are called magnetars. They typically have a dipolar magnetic field strength ~ 1015 Gauss and a mean gas density ~ 1040 cm-3 (e.g., Thompson & Duncan 1996; Frail et al. 1997). The data for extreme pulsars (magnetars) are consistent with some kind of passive frozen-in crustal magnetic dipole, of strength ~ 1027 Gauss m3. The radius of an extreme pulsar is ~ 10 km. Rotating with a period of a few seconds, with a mass ~ 1.4 solar masses, magnetars have an angular momentum ~ 1038 kg m2 s-1. When a magnetic field stronger than 1 - 14 Gauss is dragged through the pulsar crust by the diffusive motions in the pulsar core, Hall turbulence is excited and leads to multiple fractures tha will release enough energy to power soft gamma ray bursts.
The physical upper limit to the neutron star's magnetic field strength is the virial equilibrium value ~ 1018 Gauss (Lai & Salpeter, 1997).