5.1. Basic detection concepts at Radio, Extreme IR, Far IR, and Mid IR Wavelengths
How can we detect from Earth the distant interstellar magnetic fields ? Special particles affected by the magnetic field near them will emit a tell-tale polarized signal which we can capture on Earth. Thus by rotating a polarimeter attached to a radio telescope on Earth, we can detect this tell-tale polarized signal.
Figure 7 shows that high-energy relativistic electrons are trapped inside magnetic flux tubes or magnetic pipelines, in which the electrically-charged particles can glide along the lines by spiralling around them. While spiralling, they emit a synchrotron radio wave with its E-vector polarized in a direction perpendicular to the magnetic flux tube, and it is often emitted strongly at centimeter and meter wavelengths.
 |
Figure 7. High-energy relativistic electrons are trapped by a magnetic field and forced to orbit around the field line. A plaintive synchrotron (non-thermal) signal from a trapped relativistic electron is emitted strongly at meter and centimeter wavelengths. |
Figure 8 shows dust grains trapped and aligned by a magnetic field. Dust grains do emit a thermal continuum emission. The needle-like grain turns end-over-end around its center, akin to a pirouette; here the grain's short axis of rotation is aligned along the magnetic field line as proposed by some grain alignment theories - other grain alignment theories predict the grain's long axis to be aligned along the magnetic field line (e.g., Lazarian et al. 1997). The grain emits primarily in the plane of the rotation/pirouette, and its E-vector emission is polarized in a direction parallel to the grain's long axis, hence here perpendicular to the magnetic field lines. The signal is emitted strongly at Extreme IR wavelengths and at Far Infrared wavelengths.
 |
Figure 8. Elongated dust grains are aligned by an ambient magnetic field and forced to spin around the field line. A plaintive (thermal) signal from a trapped dust grain is emitted strongly at millimeter and submillimeter wavelengths. |
Original unpolarized background optical stellar light is mostly absorbed by dust if the photon's E-vector is in the plane of the grain's long axis, and mostly transmitted if the photon's E-vector is in the plane of the grain's short axis, so at optical and near Infrared wavelengths we observe more optical photons with their E-vectors parallel to the ambient magnetic field lines.
Expressing the Planck function in the optically thin régime, one gets
 |
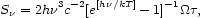where 
in steradians
is the solid angle of the source as seen from the Earth, h is the
Planck constant, and c is the speed of light and
is the
"optical" depth at frequency
, where
 |
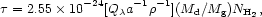with Q
is the grain emissivity, a in cm is the
grain radius, 
in g cm-3 is the grain density,
Md / Mg
0.01 is the dust mass
to grain mass in a cubic centimeter, and NH2 in
cm-2 is the column density of molecular hydrogen, and
Q = 3.8 × 10-4[250 /
]2 , with
in microns.
Hildebrand (1983)
has reviewed the derivation of dust characteristics and cloudlet
masses from submillimeter/Extreme IR thermal emission, independent of
grain models. He found that the dust mass
Md = (4/3)[a
/
Q][S D2 /
B, T], where
S is the flux
density at frequency ,
D is the distance from the Earth to the
source, B, T
is the Plank function with
frequency and temperature
T, Q
is the grain emissivity at
frequency ,
a 0.1
µm is the
grain radius,
is the grain density. Typically the value
a ~ 2.8
× 10-5 g cm-2, and the value
(4/3)[a
/ Q] ~ 0.1 g
cm-2 , at
= 250 µm.
Hence one derives:
 |
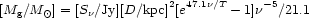where is in TeraHertz and
T is the dust temperature (e.g.,
Little et al. 1990).
For an early review, see
Heiles et al. (1991).
In addition, the first detection of a linearly polarized
(non-masing) molecular line has
been obtained with the 15m James Clerk Maxwell Telescope (JCMT) in CO
2-1 (230 GHz, 1300
microns) (e.g.,
Greaves et al. 1996).
This is a potentially useful probe of magnetic field as predicted
earlier (e.g.,
Kylafis 1983).
Here the percentage of linear polarization reaches a
maximum for an 'optical' depth near 1 but it does not depend on the
strength of the magnetic field. Also, the polarization position angle
can be independent of the magnetic field direction (for a weak magnetic
field) or else either parallel or pendicular to the magnetic field
direction (for a strong magnetic field >> 1 microGauss).
Glenn et al. (1997b)
also detected ~ 0.8% linear polarization at PA ~ - 70°
in CS 2-1 (near 3000
µm), but attributed this
amount of polarization entirely to the elongation of the envelope of the
giant branch star IRC+102216; they also claimed that the magnetic field
there is either negligible or else is
weak (<< 2 mGauss) and radially directed by the stellar wind.