


6.5. Expected B with Time
Figure 17 shows a sketch of the predicted evolution with time of the magnetic field in a dusty molecular cloudlet.
Initially (see Fig. 17a), the magnetic field is assumed to be roughly parallel to the galactic plane, where concentrations of gas and dust abound, with B ~ 10-6 Gauss and n ~ 1 cm-3. Also, interstellar turbulences, waves and shocks can travel in the galactic plane.
If the magnetic field strength is much smaller than 1 microGauss, insignificant with respect to existing interstellar turbulences, it could not act as a guide for the dust and gas.
Many theoreticians have proposed that, at a low gas density, interstellar gas and dust can accumulate or glide along magnetic field lines into denser regions, driven by magnetic instabilities, but without a noticeable increase in magnetic field strength.
Thus in this Stage I (see Fig. 17b), one could expect a gas sphere to become a gaseous sheet-like cloud, with B ~ n0.0-0.2 for n < 100 cm-3. If the magnetic field strength is much larger than 10 mGauss, it could stop the cloudlet from concentrating further and collapsing at its center due to gravitational forces, preventing the formation of substructures, i.e., cloudlets.
Our limited
magnetic field observations of large scale gas are consistent with Stage
I (k  0.1) (e.g.,
Vallée 1995a;
Vallée 1997).
0.1) (e.g.,
Vallée 1995a;
Vallée 1997).
Later, self-gravity starts, giving several elongated cloudlets inside the main cloud. Hence in this Stage II (see Fig 17c), one expects a large increase in B, with a B ~ n0.4-0.6 law for n > 100 cm-3. In Stage II, a simple model with strict mass-conserved collapse (n ~ r-3) and magnetic flux conservation (B ~ r-2) would lead to a predicted law B ~ n2/3 (excluding collisions of any kind). This is contrary to what is observed in Stage II (B ~ n1/2). So some limited flux removal mechanism may be at play in Stage II.
The observed ~ n0.5 law is predicted by many basic equilibrium models (mechanical, hierarchical, etc). In this stage, a short-lived twin outflow may appear, perpendicular to the protostellar disk. Some flux removal mechanisms in Stage II could be associated with twin magnetized bipolar outflows, magnetized disks, limited ambipolar diffusion, etc.
Some comparison can be made. Our magnetic field observations of smaller scale gas densities to date are consistent with Stage II (k ~ 0.5) (e.g., Vallée 1995a).
Much later (see Fig. 17d), a rapid decoupling of the field strength is likely to occur at a 'critical gas density' (decoupling régime, with a critical gas density n > 1012 cm-3). After a while, the magnetic field lines will slowly diffuse out of the disk, and the disk itself will slowly collapse toward the emerging protostar at its center, possibly forming some planets around the star(s). In Stage III, there are no observations yet, only observational limits.
In this research area, there is a plethora of theories on magnetic field
strength and shape, yet still not enough observations.
Mouschovias (1985)
argues that for non-self-gravitating gas with gas density n up to
n  75
cm-3 one should first allow for the
accumulation of matter along field lines, and that the
B ~ n0.5
law cannot apply there.
75
cm-3 one should first allow for the
accumulation of matter along field lines, and that the
B ~ n0.5
law cannot apply there.
There is confusion about the meaning of ambipolar diffusion. A difference of opinion and of results arises when using two different definitions for ambipolar diffusion (e.g., Shu et al. 1987, p.43). (i) The orthodox definition is that ambipolar diffusion is the process of decoupling and removal of the magnetic field from the gas, with the ensuing relatively rapid collapse of the gas to form substructures, and with strong departure from the B ~ n0.5 law in the substructures, so ambipolar diffusion starts with n > 1011 cm-3 in the substructures, while there is a decrease with time of the magnetic field. (ii) The unorthodox definition is that ambipolar diffusion can be equated with relatively slow motions even when the evolution proceeds quasi-hydrostatically, without departing from the existing B ~ n0.5 law, at n > 106 cm-3, even if the magnetic field increases with time and gas density due to contraction. The use of both definitions for ambipolar diffusion in the literature can be confusing to readers.
Mouschovias et al. (1985) employed (unorthodox) ambipolar diffusion to solve the problem that the predicted magnetic fluxes of typical stars with gas density ~ 1025 cm-3 (made from assuming flux-freezing and mass-conserving laws of the observed magnetic fluxes of corresponding masses at interstellar gas densities of ~ 105 cm-3), are far greater than the ~ 10 Gauss observed. They advocate significant ambipolar diffusion at moderately low critical gas density starting at n ~ 106 cm-3 (unorthodox definition), stop their computing near n ~ 109 cm-3, and argue that significant magnetic flux has been taken out of the central core by then. Core collisions are not included here.
This low critical gas density n for unorthodox ambipolar diffusion is not strictly in contradiction to observational data indicating that a high critical density n > 1011 cm-3 in substructures is needed for strong departure from the B ~ n0.5 law (orthodox definition) (e.g., sect. 3.3 in Davies 1994; fig. 3 in Vallée 1995a; equ. 17 in Shu et al. 1987). But processes other than ambipolar diffusion could also be at play in gas density n > 106 cm-3, such as core collisions with field amplification, magnetic line reconnections, etc.
Morton et al. (1994) gave the set of numerical equations, and a proposed numerical adaptive mesh method to solve them, for the time evolution of model cloud cores or cloudlets in a magnetic molecular cloud, at the onset of the Stage II (gas already setted in a pancake cloud; unorthodox definition of ambipolar diffusion used; no core collisions). They also found slow ambipolar diffusion, no departure from the B ~ n0.5 law, and stopped computing near n ~ 3 × 109 cm-3 (hence no stars yet).
The ambipolar diffusion timescale depends on many factors, notably charged particles (various ions, electrons, and grains of various size and charge). In cloudlets with small B values, smaller than necessary for magnetic control, grains are not lost out of the cloudlets during ambipolar diffusion (Nakano et al. 1996). In cloudlets with large B values, larger than necessary for magnetic control, grains are lost out of the cloudlets along with the magnetic field due to ambipolar diffusion in the course of cloudlet contraction by a factor 4 (e.g., Nakano 1998), because even large grains are frozen-in to the magnetic field; it follows that stars formed at the cloudlet centers, then the heavy elements in these new stars must be much less abundant than in the surrounding molecular cloudlets, and these predictions are not supported by any observations.
Christodoulou et
al. (1997)
reappraised the formal equations for gravitational
collapse in cloudlets and the viability of forming stars via core
collisions inside a cloud through coalescence. They verified that the
mass estimates correctly predict the onset of
Jeans instability in the nearby Orion starforming region as well as in
the CO cores in the disk of the Large Magellanic Cloud galaxy. The
importance of core collisions inside a cloud is thus strengthened. For
core collisions inside a cloud of volume V, having N cores
each of radius R and a velocity dispersion
 (inside the cloud), the time
t between any two core collisions is derived as
(inside the cloud), the time
t between any two core collisions is derived as
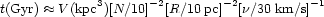 |
In addition, they found that this process predicts very little starforming activity in the halo of the Milky Way and in the halo of the Magellanic Clouds, and very little is observed (no ambipolar diffusion used).
Theoretical studies of star formation, including the magnetic fields involved, tend to use an environment made up of dense cool clouds in pressure balance with a hotter intercloud medium, while denser cores are found inside each cloud. Some of these cores may be self-gravitating, while others may be in pressure equilibrium with its surrounding. Core-core collisions followed by coalescence is expected to built up the initial core masses. Core rotation is expected, and may lead to further fragmentation (e.g., Monaghan 1983).