


8.3. Diffuse Interstellar Dust Near and in between Stars
Photons at near-IR, optical, and ultraviolet wavelengths, from 2.2
µm down to 0.12 µm, can be absorbed by
dust. The observed polarization amplitude is a function of
wavelength and varies with 2 parameters
( max,
pmax) in the modified Serkowski relation:
max,
pmax) in the modified Serkowski relation:
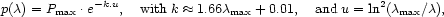 |
and pmax in % is the maximum amplitude of the polarization
found at  max
in µm (e.g.,
Whittet 1996;
Clayton et al. 1995;
Whittet et al. 1992;
Serkowski 1973).
This p(
max
in µm (e.g.,
Whittet 1996;
Clayton et al. 1995;
Whittet et al. 1992;
Serkowski 1973).
This p( ) form
is purely empirical but still reminiscent of Mie
scattering theory. Typical values are
pmax
) form
is purely empirical but still reminiscent of Mie
scattering theory. Typical values are
pmax  3% and
3% and  max
max
 0.55 µm.
0.55 µm.
It was suggested by
Martin and Whittet (1990)
that in the near-IR ( > 2.2 µm) an alternative law
p(
> 2.2 µm) an alternative law
p( )
)

 with
with

 - 1.8 might be more
representative locally.
- 1.8 might be more
representative locally.
In the far ultraviolet (~ 1500 Å; ~ 0.15 µm), half of the
polarization data have an observed value close to that predicted by the
Serkowski relation, and half of the polarization data have an excess
above the predicted value (e.g.,
Anderson et al. 1996),
which may imply that a small modification of the parameter k may be
required in the UV (k
 2.8
2.8  max).
max).
Physically, pmax is related directly to the
extinction, and thus indirectly to the distance of the star. The
p( ) curves of
stars seen through dark cloud complexes tend to exhibit a larger
) curves of
stars seen through dark cloud complexes tend to exhibit a larger
 max
max
 0.75 µm
(e.g.,
Breger et al. 1981).
Physically,
0.75 µm
(e.g.,
Breger et al. 1981).
Physically,
 max is
related to the mean size of the polarized grain.
max is
related to the mean size of the polarized grain.
Dust grains are in an active, dynamic/turbulent environment, so to keep them aligned with a magnetic field would require a significant field strength. The alignment of dust grains by the interstellar magnetic field is thought to be due to the Davis-Greenstein mechanism (paramagnetic relaxation of the spin axis of the aspherical dust grain to the direction of the ambient magnetic field), modified to include suprathermal spinup (repeated formations of H2 at the same site on a grain allowing the grain to spin up, like a spinning rocket) and superparamagnetic inclusions (small clumps of iron in a grain will give it a greater magnetic susceptibility, like a supermagnet) (e.g. Jones 1996). Hildebrand (1988a) also favors alignment of superparamagnetic grains by the modified Davis-Greenstein mechanism. Some evidence for superparamagnetic inclusions have been discussed by Martin (1995). An alternative model, that the alignment of elongated grains along the streaming motion of gas à la Gold (putting the long axis of the grain along the gas motion)or the streaming motion of photons, can be rejected (e.g., Hildebrand 1988b), since streaming of gas along the galactic plane would put the long axis of the grain along the galactic plane, hence the E-vector of the optical polarization observed will be perpendicular to the galactic plane due to preferential absorption of light, contrary to what is observed (e.g., Hildebrand 1989).
Chemically, the respective amounts of carbonaceous and graphite grains
(optical hump effects) versus silicate grains (near-IR and optical
effects) and their effects on
 max are
still being debated. In the Far-UV, the extinction data seem to require
the presence of a mixture of many PAH (Polycyclic Aromatic Hydrocarbons)
(e.g.,
Li and Greenberg 1997).
max are
still being debated. In the Far-UV, the extinction data seem to require
the presence of a mixture of many PAH (Polycyclic Aromatic Hydrocarbons)
(e.g.,
Li and Greenberg 1997).
To B or not to B ? Some optical/near-infrared polarization
maps were made of nearby cloudlets, notably Ophiuchi (e.g.,
Bastien and Ménard 1990;
Goodman et al. 1990),
using stars at specified locations. Linear polarization maps of Young
Stellar Objects with a pattern of aligned polarization vectors at
optical wavelengths as observed very close to the central object have
been interpreted in terms of multiple scattering in flattened optically
thick structures, not in terms of magnetically aligned elongated grains
(Bastien and Ménard
1990).
These optical patterns provide direct evidence for circumstellar disks
around YSO. Optical/near-infrared polarization mapping can indicate
large dust scattering effects, saying nothing about the magnetic
field. Optical polarization mapping can best be done for the more nearby
cloudlets (distant from the Earth by < 1 kpc). Optical polarization
maps due to dust scattering can tell us more about the distribution and
structure of dust grains
(polarization position angles) and about grain sizes (polarization
percentages) (e.g.,
Fischer 1995),
but nothing on magnetic fields.
Casali (1995)
observed at near-IR
( 1.25 µm
to
1.25 µm
to  2.2 µm)
some 33 young stellar objects in L1641 dark cloud (size of
10 × 40 pc),
and found a huge random orientation of the E-vector polarization
position angles, telling us nothing on the
link between these YSO and the cloud's magnetic field in most clouds
(Goodman et al. 1995).
Carlqvist and Kristen
(1997)
summed up a numerical study of magnetic fields in filaments as
seen at optical and near IR wavelengths, by finding that it is difficult
to figure out the geometry of the magnetic field from optical/near IR
polarization observations, and also difficult to determine the strength
of the magnetic field.
2.2 µm)
some 33 young stellar objects in L1641 dark cloud (size of
10 × 40 pc),
and found a huge random orientation of the E-vector polarization
position angles, telling us nothing on the
link between these YSO and the cloud's magnetic field in most clouds
(Goodman et al. 1995).
Carlqvist and Kristen
(1997)
summed up a numerical study of magnetic fields in filaments as
seen at optical and near IR wavelengths, by finding that it is difficult
to figure out the geometry of the magnetic field from optical/near IR
polarization observations, and also difficult to determine the strength
of the magnetic field.
There are exceptions. Tamura et al. (1996) have found one cloud where they claim the opposite, namely that near Infrared polarimetry does reveal the magnetic field in the dark cloud. The existing bank of optical polarization observations of stars near cloudlets along 8000 lines of sight (e.g., Axon and Ellis 1976; Bastien 1996) could be of use in comparing with radio polarization data, althought optical stars exactly behind dark cloudlets will not be seen at optical wavelengths. This comparison is not often made.
Fortunately, Extreme-IR (submillimeter), Far IR, and mid-IR wavelength
polarization observations, and all mapping at long wavelengths
 , involve no dust
scattering, since scattering varies with the
wavelength
, involve no dust
scattering, since scattering varies with the
wavelength  as
as
 -4 (e.g.,
Tamura et al. 1988;
Tamura et al. 1993;
Bhatt and Jain 1992).
Thus the emission component seen is the true component, along the
line of sight.
-4 (e.g.,
Tamura et al. 1988;
Tamura et al. 1993;
Bhatt and Jain 1992).
Thus the emission component seen is the true component, along the
line of sight.