Copyright © 1996 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1996. 34:
461-510 Copyright © 1996 by Annual Reviews. All rights reserved |
2.4. Uncertainty in LTO Due to the Assumed Chemistry of Stars
It has long been known that the predicted age of
a star of a given mass depends on its initial helium and heavy-element
abundances
(e.g. Demarque 1967,
Iben & Rood
1970).
Even the special importance of the CNO elements for stellar ages was
appreciated early on (e.g.
Simoda & Iben
1968).
This has driven a huge, ongoing effort by many observers to define the
detailed run of chemical abundances in field and halo stars as
accurately as possible.
Thanks to that effort, we now know (for instance) that [C/Fe] and [N/Fe]
~ 0 over 0.3  [Fe/H]
[Fe/H]  -2 and that the elements synthesized by
-2 and that the elements synthesized by
 -capture
processes (e.g. O, Ne, Mg, Si, etc) are enhanced, relative to iron, in
metal-poor stars by a factor of 2-3 (see the comprehensive review by
Wheeler, Sneden &
Truran 1989).
(In the standard notation, this corresponds to
[
-capture
processes (e.g. O, Ne, Mg, Si, etc) are enhanced, relative to iron, in
metal-poor stars by a factor of 2-3 (see the comprehensive review by
Wheeler, Sneden &
Truran 1989).
(In the standard notation, this corresponds to
[ /Fe]
/Fe]
 0.3-0.5, where
0.3-0.5, where
 represents O or Ne or
Mg, etc.) It is not yet definite that all of the so-called
represents O or Ne or
Mg, etc.) It is not yet definite that all of the so-called
 -elements
scale together as there is considerable scatter in the field star
observations
(some of it real): Thus, the precise shapes of the mean relations between
the various [element/Fe] ratios as a function of [Fe/H] still have some
degree
of uncertainty. Also, whether or not field and GC dwarfs of the same iron
content are chemically indistinguishable remains a matter of some concern.
But the chemistry of stars appears to be largely under control.
-elements
scale together as there is considerable scatter in the field star
observations
(some of it real): Thus, the precise shapes of the mean relations between
the various [element/Fe] ratios as a function of [Fe/H] still have some
degree
of uncertainty. Also, whether or not field and GC dwarfs of the same iron
content are chemically indistinguishable remains a matter of some concern.
But the chemistry of stars appears to be largely under control.
High-resolution spectroscopy (e.g.
Cohen 1979,
Sneden et al
1991)
and the tightness of observed CMDs (e.g.
Stetson 1993;,
Folgheraiter, Penny
& Griffiths 1993)
have established that the dispersion in Fe abundances is very small in
nearly all GCs ( Cen and
possibly M22 being exceptions). Moreover, the spectroscopic data now
yield [Fe/H] values that are accurate to within
Cen and
possibly M22 being exceptions). Moreover, the spectroscopic data now
yield [Fe/H] values that are accurate to within
 ± 0.2 dex, if not
better. According to the upper panel of Figure 4
- which shows plots of the turnoff luminosity versus age relations that
VandenBerg et al
(1996) have computed for various choices of [Fe/H],
[
± 0.2 dex, if not
better. According to the upper panel of Figure 4
- which shows plots of the turnoff luminosity versus age relations that
VandenBerg et al
(1996) have computed for various choices of [Fe/H],
[ /Fe], and Y
- this implies an uncertainty in the age at a given M
bol(TO) of about ± 1 Gyr
(
/Fe], and Y
- this implies an uncertainty in the age at a given M
bol(TO) of about ± 1 Gyr
( ±
7%). Furthermore, since the
±
7%). Furthermore, since the
 -element contents of
stars in the extremely metal-deficient clusters like M92 appear to be
within ± 0.15 dex of
[
-element contents of
stars in the extremely metal-deficient clusters like M92 appear to be
within ± 0.15 dex of
[ /Fe] = 0.4 (e.g.
Sneden et al
1991;,
McWilliam, Geisler
& Rich 1992), the corresponding age uncertainty is expected to
be about ± 4% (judging from Figure 4). This
makes a total uncertainty of ± 11% in the turnoff ages due to
current errors in heavy-element abundance determinations.
4
/Fe] = 0.4 (e.g.
Sneden et al
1991;,
McWilliam, Geisler
& Rich 1992), the corresponding age uncertainty is expected to
be about ± 4% (judging from Figure 4). This
makes a total uncertainty of ± 11% in the turnoff ages due to
current errors in heavy-element abundance determinations.
4
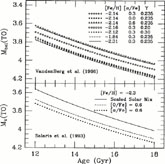 |
Figure 4. Turnoff luminosity vs age relations for various chemical composition parameters. |
Helium-abundance uncertainties could potentially affect age estimates at
the few percent level (see the upper panel of
Figure 4), but Y
appears to be rather well determined, in spite of the fact that the methods
used are indirect. [Spectral features due to helium can be detected in hot
HB stars, but gravitational settling is known to be important in them (e.g.
Heber et al 1986).]
Foremost among these techniques is the so-called R-method
(Iben 1968b),
which compares the ratio of the predicted HB and RGB lifetimes,
tHB / tRGB, as a function of
Y, with the observed number ratio of stars in these phases. Using
mainly the calibration of
Buzzoni et al
(1983)
(also see
Caputo, Martinez Roger
& Paez 1987), nearly all applications of the R-method (e.g.
Buonanno, Corsi &
Fusi Pecci 1985;,
Ferraro et al
1992,
1993)
have yielded Y = 0.23 ± 0.02. Discrepant results have been
obtained for a few globulars, such as M68
(Walker 1994),
for which the R-method implies Y ~
0.17; however, in that particular case, the analogous ratio of the numbers
of asymptotic-giant branch to RGB stars gives an estimate of the helium
abundance
that is within 1  of
Y = 0.23. (Why M68 has such an anomalous R value is presently
unknown.)
of
Y = 0.23. (Why M68 has such an anomalous R value is presently
unknown.)
Fits to the morphologies of observed HB populations (e.g.
Dorman, VandenBerg
& Laskarides 1989;,
Dorman, Lee &
VandenBerg 1991)
and to the red edges of the RR Lyrae instability strips in clusters
(Bono et al 1995)
reinforce the R-method results. Pulsation models have traditionally
favored Y
 0.30, but due to the
advent of the OPAL
(Rogers &
Iglesias 1992) and OP
(Seaton et al
1994)
opacities, lower values of Y can now be accommodated
(Kovács et al
1992,
Cox 1995).
The adoption of Y
0.30, but due to the
advent of the OPAL
(Rogers &
Iglesias 1992) and OP
(Seaton et al
1994)
opacities, lower values of Y can now be accommodated
(Kovács et al
1992,
Cox 1995).
The adoption of Y
 0.23 in models for GC stars is further supported by the fact that this value
is very close to that predicted by standard and inhomogeneous Big Bang
nucleosynthesis calculations (see, e.g.
Krauss &
Romanelli 1990,
Mathews, Schramm
& Meyer 1993,
respectively), as well as empirical determinations of the pregalactic
helium abundance
(Pagel et al
1992;,
Izotov, Thuan &
Lipovetsky 1994;,
Olive & Steigman
1995).
0.23 in models for GC stars is further supported by the fact that this value
is very close to that predicted by standard and inhomogeneous Big Bang
nucleosynthesis calculations (see, e.g.
Krauss &
Romanelli 1990,
Mathews, Schramm
& Meyer 1993,
respectively), as well as empirical determinations of the pregalactic
helium abundance
(Pagel et al
1992;,
Izotov, Thuan &
Lipovetsky 1994;,
Olive & Steigman
1995).
We conclude this section by emphasizing the importance of oxygen to
stellar age determinations. Plotted in the lower panel of
Figure 4 are the age versus turnoff luminosity
relations that
Salaris et al
(1993)
have derived for [Fe/H] = -2.3 and various assumptions about the
element mix. This plot shows that most of the reduction in age at a
given LTO that results from an enhancement in the
 -elements
is due to oxygen. Getting the oxygen abundance right is, therefore, a much
bigger concern than having precise abundances for most of the other heavy
elements. This result is not unexpected given the large abundance of oxygen
and its role as a catalyst in the CNO-cycle and as a major contributor to
bound-free opacities in stellar interiors (see, e.g.
VandenBerg 1992).
-elements
is due to oxygen. Getting the oxygen abundance right is, therefore, a much
bigger concern than having precise abundances for most of the other heavy
elements. This result is not unexpected given the large abundance of oxygen
and its role as a catalyst in the CNO-cycle and as a major contributor to
bound-free opacities in stellar interiors (see, e.g.
VandenBerg 1992).
4 At first sight,
Figure 4 would appear to contradict the
claim by
Chieffi, Straniero
& Salaris (1991) that enhancements in the
 -elements do not lead to
younger ages for the GCs (also see
Bencivenni et al
1991).
But, in fact, the reason why they obtained similar ages using either
-elements do not lead to
younger ages for the GCs (also see
Bencivenni et al
1991).
But, in fact, the reason why they obtained similar ages using either
 -enhanced or
scaled-solar abundance isochrones is that they set the distances to the
globulars using theoretical horizontal-branch calculations, which
predict that the HB luminosity should decrease as
[
-enhanced or
scaled-solar abundance isochrones is that they set the distances to the
globulars using theoretical horizontal-branch calculations, which
predict that the HB luminosity should decrease as
[ / Fe] increases. Only
by an appropriate adjustment of the GC distance scale is it possible to
reach the conclusion that ages are insensitive to
[
/ Fe] increases. Only
by an appropriate adjustment of the GC distance scale is it possible to
reach the conclusion that ages are insensitive to
[ / Fe]: The turnoff
age-luminosity relations computed by
Salaris, Chieffi
& Straniero (1993) both for
[
/ Fe]: The turnoff
age-luminosity relations computed by
Salaris, Chieffi
& Straniero (1993) both for
[ / Fe] = 0.0 and for
[
/ Fe] = 0.0 and for
[ / Fe] > 0.0 are
very similar to those derived by
VandenBerg et al
(1996).
Back.
/ Fe] > 0.0 are
very similar to those derived by
VandenBerg et al
(1996).
Back.