


We have seen that radio sources have a profound effect on the X-ray-emitting ICM, inflating bubbles that rise buoyantly into the clusters. But, is the energy deposition into the ICM from the radio sources sufficient to account for the lack of gas seen at very low temperatures in cooling flow clusters? Using the pressures of the X-ray-bright shells surrounding the bubbles, and the volumes of the bubbles, we can determine the total energy output of a radio source. The energy output includes both the internal energy of the bubble and the work done to expand the bubble. From Churazov et al. (2002), the total energy required for a radio source to inflate a bubble in the ICM is
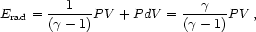 |
(1) |
where V is the volume of the bubble, and
 is the
mean adiabatic index of the fluid in the bubble (5/3 for
non-relativistic gas or 4/3 for relativistic gas).
To get the average rate of energy input from a central radio source, we
divide this energy by the repetition rate of the radio source, based on the
buoyancy rise time of ghost cavities, and with a value of approximately
108 yr (see Section 5).
We compare this energy input rate with the luminosity of cooling gas derived
from spectral fitting to the X-ray data. The luminosity of isobaric
cooling gas is given by
is the
mean adiabatic index of the fluid in the bubble (5/3 for
non-relativistic gas or 4/3 for relativistic gas).
To get the average rate of energy input from a central radio source, we
divide this energy by the repetition rate of the radio source, based on the
buoyancy rise time of ghost cavities, and with a value of approximately
108 yr (see Section 5).
We compare this energy input rate with the luminosity of cooling gas derived
from spectral fitting to the X-ray data. The luminosity of isobaric
cooling gas is given by
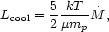 |
(2) |
where kT is the temperature of the ICM outside of the cooling region,
 is the mass-deposition rate, and µ is the mean mass per
particle in units of the proton mass.
is the mass-deposition rate, and µ is the mean mass per
particle in units of the proton mass.
For the case of Hydra A
(McNamara et al. 2000;
David et al. 2001;
Nulsen et al. 2002),
the total power output of the radio source, derived as
described above from the X-ray pressure and volumes of the radio cavities,
is 2.7 × 1044 erg s-1. The cooling
luminosity, using
 = 300
M
= 300
M yr-1 and kT = 3.4 keV, is
Lcool = 3 × 1044 erg
s-1. Therefore, in this case,
just based on these simple energy arguments,
the radio source is depositing enough energy into the ICM on average
to offset the cooling gas. A similar test performed for Abell 2052
(Blanton et al. 2003)
shows that the radio source also has sufficient power
(3 × 1043 erg s-1) to offset the cooling gas
(Lcool = 3 × 1043 erg s-1 with
yr-1 and kT = 3.4 keV, is
Lcool = 3 × 1044 erg
s-1. Therefore, in this case,
just based on these simple energy arguments,
the radio source is depositing enough energy into the ICM on average
to offset the cooling gas. A similar test performed for Abell 2052
(Blanton et al. 2003)
shows that the radio source also has sufficient power
(3 × 1043 erg s-1) to offset the cooling gas
(Lcool = 3 × 1043 erg s-1 with
 = 42
M
= 42
M yr-1 and kT = 3 keV). The situation is different for
Abell 262
(Blanton et al., in preparation),
where the radio source power
(3.4 × 1041 erg s-1)
falls more than an order of magnitude short of that required to offset
the cooling luminosity (Lcool = 1.3 ×
1043 erg s-1,
using kT = 2.65 keV, and the mass-deposition rate of
18.8 M
yr-1 and kT = 3 keV). The situation is different for
Abell 262
(Blanton et al., in preparation),
where the radio source power
(3.4 × 1041 erg s-1)
falls more than an order of magnitude short of that required to offset
the cooling luminosity (Lcool = 1.3 ×
1043 erg s-1,
using kT = 2.65 keV, and the mass-deposition rate of
18.8 M yr-1). However, this radio source is much less
luminous than Hydra A or 3C 317 in Abell 2052, and the bubble volume inflated in Abell 262 is
much smaller than that in the others. The bubble diameter is only 5 kpc in
Abell 262 compared to diameters of 20 - 25 kpc for
the others. Since
we are assuming that the power output from the radio source is an average,
over many outbursts of the AGN, it may be that a previous outburst of
the radio source in Abell 262 was much more powerful, so that, on average,
the cooling could still be balanced by the input of energy from the
radio source.
yr-1). However, this radio source is much less
luminous than Hydra A or 3C 317 in Abell 2052, and the bubble volume inflated in Abell 262 is
much smaller than that in the others. The bubble diameter is only 5 kpc in
Abell 262 compared to diameters of 20 - 25 kpc for
the others. Since
we are assuming that the power output from the radio source is an average,
over many outbursts of the AGN, it may be that a previous outburst of
the radio source in Abell 262 was much more powerful, so that, on average,
the cooling could still be balanced by the input of energy from the
radio source.