


From the above discussion, it is clear that theorists are in desperate need of further input from experiment - in particular, we need to know if the dark energy is constant or dynamical, and if it is dynamical what form it takes. The observational program to test these ideas has been discussed in detail elsewhere (Sahni & Starobinski 2000, Carroll 2001, Peebles & Ratra 2003); here we briefly draw attention to a couple of theoretical issues which can affect the observational strategies.
4.1. Equation-of-state parameter
Given that the universe is accelerating, the next immediate question is whether the acceleration is caused by a strictly constant vacuum energy or something else; the obvious place to look is for some time-dependence to the dark energy density. In principle any behavior is possible, but it is sensible to choose a simple parameterization which would characterize dark energy evolution in the measurable regime of relatively nearby redshifts (order unity or less). For this purpose it is common to imagine that the dark energy evolves as a power law with the scale factor:
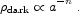 |
(1.36) |
Even if
 dark
is not strictly a power law, this ansatz
can be a useful characterization of its effective behavior at
low redshifts. We can then define an equation-of-state
parameter relating the energy density to the pressure,
dark
is not strictly a power law, this ansatz
can be a useful characterization of its effective behavior at
low redshifts. We can then define an equation-of-state
parameter relating the energy density to the pressure,
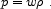 |
(1.37) |
Using the equation of energy-momentum conservation,
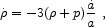 |
(1.38) |
a constant exponent n of (1.36) implies a constant w with
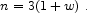 |
(1.39) |
As n varies from 3 (matter) to 0 (cosmological constant), w
varies from 0 to -1.
Some limits from supernovae, large-scale structure, and the CMB from
Melchiorri, Mersini,
Ödman & Trodden 2003
are shown in Figure (3); see
Spergel et al 2003
for limits from WMAP observations of the cosmic microwave background,
Schuecker et al. 2003
for limits from X-ray clusters,
and Tonry et al. 2003
and Knop et al. 2003
for more recent supernova limits. These constraints apply to the
 M-w
plane, under the assumption that the universe is flat
(
M-w
plane, under the assumption that the universe is flat
( M +
M +
 dark =
1). We see that the observationally favored region features
dark =
1). We see that the observationally favored region features
 M
M
 0.3 and an honest
cosmological constant, w = -1. However, there
is room for alternatives; one of the most important tasks
of observational cosmology will be to reduce the error regions on plots
such as this to pin down precise values of these parameters.
0.3 and an honest
cosmological constant, w = -1. However, there
is room for alternatives; one of the most important tasks
of observational cosmology will be to reduce the error regions on plots
such as this to pin down precise values of these parameters.
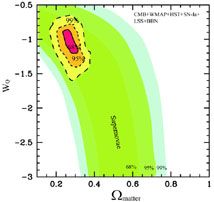 |
Figure 3. Limits on the equation-of-state
parameter w in a flat universe,
where |
It is clear that w = -1 is a special value; for w > -1 the
dark energy density slowly decreases as the universe expands,
while for w < -1 it would actually be increasing. In most
conventional models, unsurprisingly, we have w
 -1; this is
also required (for sources with positive energy densities) by
the energy conditions of general relativity
(Garnavich et al. 1998).
Nevertheless, it is interesting to ask whether we should bother to
consider w < -1
(Parker & Raval 1999,
Sahni & Starobinski
2000,
Caldwell 2002,
Carroll, Hoffman &
Trodden 2003).
If w is constant in such a model, the universe will
expand ever faster until a future singularity is reached, the
"Big Rip"
(Caldwell, Kamionkowski
& Weinberg 2003);
but such behavior is by no means necessary. An explicit model
is given by so-called phantom fields
(Caldwell 2002),
scalar fields with negative kinetic and gradient energy,
-1; this is
also required (for sources with positive energy densities) by
the energy conditions of general relativity
(Garnavich et al. 1998).
Nevertheless, it is interesting to ask whether we should bother to
consider w < -1
(Parker & Raval 1999,
Sahni & Starobinski
2000,
Caldwell 2002,
Carroll, Hoffman &
Trodden 2003).
If w is constant in such a model, the universe will
expand ever faster until a future singularity is reached, the
"Big Rip"
(Caldwell, Kamionkowski
& Weinberg 2003);
but such behavior is by no means necessary. An explicit model
is given by so-called phantom fields
(Caldwell 2002),
scalar fields with negative kinetic and gradient energy,
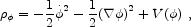 |
(1.40) |
in contrast with the conventional expression (1.26). (A phantom may be thought of as a physical realization of the "ghost" fields used in some calculations in quantum field theory.) A phantom field rolls to the maximum of its potential, rather than the minimum; if there is a maximum with positive potential energy, we will have w < -1 while the field is rolling, but it will settle into a state with w = -1.
However, such fields are very dangerous in particle physics; the excitations of the phantom will be negative-mass particles, and therefore allow for the decay of empty space into a collection of positive-energy ordinary particles and negative-energy phantoms. Naively the decay rate is infinite, because there is no boundary to the allowed phase space; if we impose a cutoff by hand by disallowing momenta greater than 10-3 eV, the vacuum can be stable for the age of the universe (Carroll, Hoffman & Trodden 2003). Of course, there may be other ways to get w < -1 other than a simple phantom field (Parker & Raval 1999, Dvali & Turner 2003), and there is a lurking danger that a rapidly time-varying equation of state might trick you into thinking that w < -1 (Maor, Brustein, McMahon, & Steinhardt, 2002). The moral of the story should be that theorists proposing models with w < -1 should be very careful to check that their theories are sufficiently stable, while observers should be open-minded and include w < -1 in the parameter space they constrain. To say the least, a convincing measurement that the effective value of w were less than -1 would be an important discovery, the possibility of which one would not want to exclude a priori.