3. INTERSTELLAR REDDENING

Our knowledge of interstellar dust is largely derived from the interaction of dust particles with electromagnetic radiation: attenuation of starlight, scattering of light, and emission of infrared and far-infrared radiation.

The wavelength dependence of interstellar extinction tells us about both the size and composition of the grains. The extinction is best determined using the "pair method" - comparison of the fluxes from two stars with nearly-identical spectroscopic features (and therefore photospheric temperature and gravity) but with one of the stars nearly unaffected by dust. With the assumption that the extinction goes to zero as wavelength , it is possible to determine the extinction A as a function of wavelength (see, e.g., Fitzpatrick & Massa 1990, and references therein).

The extinction A is obviously proportional to the amount of dust, but A / A₀, the extinction normalized to some reference wavelength , characterizes the kind of dust present, and its size distribution. The quantity R_V A_V / (A_B - A_V) characterizes the slope of the extinction curve between V = 0.55 µm and B = 0.44 µm; small values of R_V correspond to steep extinction curves.

In principle, the function A / A₀ is unique to every sightline, but Cardelli et al. (1989) found that the observed A / A₀ can be approximated by a one-parameter family of curves: A / A₀ = f(, R_V), where they chose R_V A_V / (A_B - A_V) as the parameter because it varies significantly from one curve to another. Cardelli et al. obtained functional forms for f(, R_V) which provided a good fit to observational data; Fitzpatrick (1999) revisited this question and, explicitly correcting for the finite width of photometric bands, obtained a slightly revised set of fitting functions. Figure 1 shows the Fitzpatrick (1999) fitting functions, using I_C = 0.802 µm, the central wavelength of the Cousins I band, as the reference wavelength. The parameterization is shown for values of R_V ranging from 2.1 to 5.5, which spans the range of R_V values encountered on sightlines through diffuse clouds in the Milky Way. Also shown is an empirical fit to the extinction measured toward HD210121, showing how an individual sightline can deviate from the one-parameter fitting function f(, R_V).

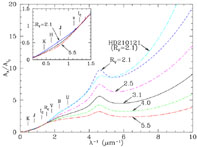Figure 1. Extinction normalized to Cousins I band extinction for RV values ranging from 2.1 to 5.5, using the Fitzpatrick (1999) parameterization, plus diffuse interstellar bands following Jenniskens & Desert (1994). Also shown is an improved fit to the extinction curve toward HD21021, providing one example of how a sightline can deviate from the average behavior for the same value of RV.

Dust on sightlines with different values of R_V obviously must have either different compositions or different size distributions, or both. Also of interest is the total amount of dust per unit H. This requires measurement of the total H column density N_H N(H) + 2N(H₂) + N(H⁺). On most sightlines the ionized hydrogen is a small correction; N(H) and N(H₂) can be measured using ultraviolet absorption lines.

Rachford et al. (2002) determined N_H to an estimated accuracy of better than a factor 1.5 on 14 sightlines. It appears that A_I / N_H is positively correlated with R_V, with

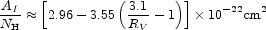(1)

providing an empirical fit (Draine 2003a). We can use the Fitzpatrick (1999) parameterization and equation (1) to estimate A / N_H for sightlines with different R_V. The results are shown in Figure 2 - sightlines with larger R_V values appear to have larger values of A / N_H for ^-1 3 µm^-1, and decreased values for ^-1 4 µm^-1. This is interpreted as resulting from coagulation of a fraction of the smallest grains onto the larger grains; loss of small grains decreases the ultraviolet extinction, while adding mass to the larger grains increases the scattering at 0.3 µm.

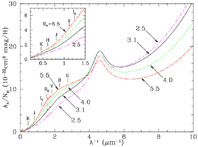Figure 2. Extinction per unit H column density, for different RV. From Draine (2003a).