3. UNDERSTANDING TIME DELAYS: A GENERAL THEORY

The need to model the gravitational potential of the lens is the aspect of interpreting time delays that creates the greatest suspicion. The most extreme view is that it renders the project "hopeless" because we will never be able to guarantee that the models encompass the degrees of freedom needed to capture all the systematic uncertainties. In order to address these fears we must show that we understand the specific properties of the gravitational potential determining time delays and then ensure that our parameterized models include these degrees of freedom.

The examples we considered in Section 2 illustrate the basic physics of time delays, but an extensive catalog of (non)parametric models demonstrating the same properties may not be convincing to the skeptic. We will instead show, using standard mathematical expansions of the potential, which properties of the lens galaxy are required to understand time delays with accuracies of a few percent. While we can understand the results of all models for the time delays of gravitational lenses based on this simple theory, full numerical models should probably be used for most detailed, quantitative analyses. Fortunately, there are publically available programs for both the parametric and nonparametric approaches. ⁽³⁾ Our analysis uses the geometry of the schematic lens shown in Figure 1. The two images define an annulus bounded by their radii, R_A and R_B, and with an interior region for R < R_B and an exterior region for R > R_A.

The key to understanding time delays comes from Gorenstein, Falco, & Shapiro (1988; see also Saha 2000), who showed that the time delay of a circular lens depends only on the image positions and the surface density (R) in the annulus between the images. The mass of the interior region is implicit in the image positions and accurately determined by the astrometry. From Gauss' law, we know that the radial distribution of the mass in the interior region and the amount or distribution of mass in the exterior region is irrelevant. A useful approximation is to assume that the surface density in the annulus can be locally approximated by a power law R^1- and that the mean surface density in the annulus is <> = <> / _c. The time delay between the images is (Kochanek 2002)

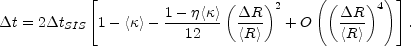(7)

Thus, the time delay is largely determined by the average density <>, with only modest corrections from the local shape of the surface density distribution even when R / <R> 1. For example, the second-order expansion is exact for an SIS lens (<> = 1/2, = 2) and reproduces the time delay of a point mass lens (<> = 0) to better than 1% even when R / <R> = 1. This local model also explains the time delay scalings of the global power-law models we discussed in Section 2. A r^- global power law has surface density <> = (3 - ) / 2 near the Einstein ring, so the leading term of the time delay is t = 2 t_SIS(1 - <>) = ( - 1) t_SIS, just as in Equation (6).

• The time delay is not determined by the global structure of the radial density profile but rather by the surface density near the Einstein ring.

Gorenstein et al. (1988) considered only circular lenses, but a multipole expansion allows us to understand the role of angular structure (Kochanek 2002). An estimate to the same order as in Equation (7) requires only the quadrupole moments of the regions interior and exterior to the annulus, provided the strengths of the higher-order multipoles of the potential have the same order of magnitude as for an ellipsoidal density distribution. ⁽⁴⁾ This approximation can fail for the lenses in clusters (see Section 4). The complete expansion for t when the two quadrupole moments have independent amplitudes and orientations is not very informative. However, the leading term of the expansion when the two quadrupole moments are aligned illustrates the role of angular structure. Given an exterior quadrupole (i.e., an external shear) of amplitude _ext and an interior quadrupole of amplitude _int sharing a common axis , the quadrupole potential is

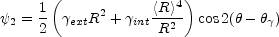(8)

if we define the amplitudes at radius <R>. For images at positions R_A(cos _A, sin _A) and R_B(cos _B, sin _B) relative to the lens galaxy (see Fig. 1), the leading term of the time delay is

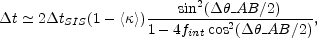(9)

where _AB = _A - _B and f_int = _int / (_ext + _int) is the fraction of the quadrupole due to the interior quadrupole moment _int. We need not worry about the possibility of a singular denominator - successful global models of the lens do not allow such configurations.

A two-image lens has too few astrometric constraints to fully constrain a model with independent, misaligned internal and external quadrupoles. Fortunately, when the lensed images lie on opposite sides of the lens galaxy ( _AB + , || << 1), the time delay becomes insensitive to the quadrupole structure. Provided the angular deflections are smaller than the radial deflections (||<R> R), the leading term of the time delay reduces to the result for a circular lens, t 2 t_SIS(1 - <>). There is, however, one limiting case to remember. If the images and the lens are colinear, as in a spherical lens, the component of the shear aligned with the separation vector acts like a contribution to the convergence. In most lenses this would be a modest additional uncertainty - in the typical lens these shears must be small, the sign of the effect should be nearly random, and it is only a true degeneracy in the limit that everything is colinear.

A four-image lens has more astrometric constraints and can constrain a model with independent, misaligned internal and external quadrupoles. The quadrupole moments of the observed lenses are dominated by external shear, with f_int 1/4 unless there is more than one lens galaxy inside the Einstein ring. The ability of the astrometry to constrain f_int is important because the delays depend strongly on f_int when the images do not lie on opposite sides of the galaxy. If external shears dominate, f_int 0 and the leading term of the delay becomes t 2 t_SIS(1 - <>) sin² _AB/2. If the model is isothermal, like the = rF() models we considered in Section 2, then f_int = 1/4 and we again find that the delay is independent of the angle, with t 2 t_SIS(1 - <>). The time delay ratios in a four-image lens are largely determined by the angular structure and provide a check of the potential model.

In summary, if we want to understand time delays to an accuracy competitive with studies of the local distance scale (5%-10%), the only important variable is the surface density <> of the lens in the annulus between the images. When models based on the same data for the time delay and the image positions predict different values for H₀, the differences can always be understood as the consequence of different choices for <>. In parametric models <> is adjusted by changing the central concentration of the lens (i.e., like in the global power-law models), and in the nonparametric models of Williams & Saha (2000) it is adjusted directly. The expansion models of Zhao & Qin (2003a, b) mix aspects of both approaches.

³ The gravlens and lensmodel (Keeton 2003, cfa-www.harvard.edu/~castles) packages include a very broad range of parametric models for the mass distributions of lenses, and the PixelLens package (Williams & Saha 2000, ankh-morpork.maths.qmw.ac.uk/~saha/astron/lens/pix/) implements a nonparametric approach. Back.

⁴ If the quadrupole potential, ₂ cos 2, has dimensionless amplitude ₂, then it produces ray deflections of order O(₂ b) at the Einstein ring of the lens. In a four-image lens the quadrupole deflections are comparable to the thickness of the annulus, so ₂ R / <R>. In a two-image lens they are smaller than the thickness of the annulus, so ₂ R / <R>. For an ellipsoidal density distribution, the cos(2m) multipole amplitude scales as _2m ~ ₂^m (R / <R>)^m. This allows us to ignore the quadrupole density distribution in the annulus and all higher-order multipoles. It is important to remember that potentials are much rounder than surface densities [with relative amplitudes for a cos(m ) multipole of roughly m^-2:m^-1:1 for potentials:deflections:densities], so the multipoles relevant to time delays converge rapidly even for very flat surface density distributions. Back.