


This section discusses some ways in which the standard model could be extended. At present, there is no positive evidence in favor of any of these possibilities, which are becoming increasingly constrained by the data, though there always remains the possibility of trace effects at a level below present observational capability.
2.1. More general perturbations
The standard cosmology assumes adiabatic, Gaussian perturbations. Adiabaticity means that all types of material in the Universe share a common perturbation, so that if the space-time is foliated by constant-density hypersurfaces, then all fluids and fields are homogeneous on those slices, with the perturbations completely described by the variation of the spatial curvature of the slices. Gaussianity means that the initial perturbations obey Gaussian statistics, with the amplitudes of waves of different wavenumbers being randomly drawn from a Gaussian distribution of width given by the power spectrum. Note that gravitational instability generates non-Gaussianity; in this context, Gaussianity refers to a property of the initial perturbations before they evolve significantly.
The simplest inflation models based on one dynamical field predict adiabatic fluctuations and a level of non-Gaussianity which is too small to be detected by any experiment so far conceived. For present data, the primordial spectra are usually assumed to be power laws.
For typical inflation models, it is an approximation to take the spectra as
power laws, albeit usually a good one. As data quality improves, one might
expect this approximation to
come under pressure, requiring a more accurate description of the initial
spectra, particularly for the density perturbations. In general, one can
write a Taylor expansion of
ln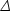 2
2 as
as
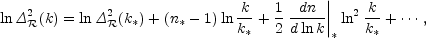
| (1.9) |
where the coefficients are all evaluated at some scale k*. The term dn / d ln k|* is often called the running of the spectral index [9], and has recently become topical due to a possible low-significance detection by WMAP. Once non-power-law spectra are allowed, it is necessary to specify the scale k* at which quantities such as the spectral index are defined.
2.1.2. Isocurvature perturbations
An isocurvature perturbation is one which leaves the total density unperturbed, while perturbing the relative amounts of different materials. If the Universe contains N fluids, there is one growing adiabatic mode and N - 1 growing isocurvature modes. These can be excited, for example, in inflationary models where there are two or more fields which acquire dynamically important perturbations. If one field decays to form normal matter, while the second survives to become the dark matter, this will generate a cold dark matter isocurvature perturbation.
In general there are also correlations between the different modes, and so the full set of perturbations is described by a matrix giving the spectra and their correlations. Constraining such a general construct is challenging, though constraints on individual modes are beginning to become meaningful, with no evidence that any other than the adiabatic mode must be non-zero.
Multi-field inflation models can also generate primordial non-Gaussianity. The extra fields can either be in the same sector of the underlying theory as the inflaton, or completely separate, an interesting example of the latter being the curvaton model [10]. Current upper limits on non-Gaussianity are becoming stringent, but there remains much scope to push down those limits and perhaps reveal trace non-Gaussianity in the data. If non-Gaussianity is observed, its nature may favor an inflationary origin, or a different one such as topological defects. A plausible possibility is non-Gaussianity caused by defects forming in a phase transition which ended inflation.