


Although it contains two ingredients - dark matter and dark energy - which
have not yet been verified by laboratory experiments, the
 CDM model is
almost universally
accepted by cosmologists as the best description of present data. The basic
ingredients are given by the parameters listed in
Sec. 1.4, with
approximate values of some of the key parameters being
CDM model is
almost universally
accepted by cosmologists as the best description of present data. The basic
ingredients are given by the parameters listed in
Sec. 1.4, with
approximate values of some of the key parameters being
 b
b
 0.04,
0.04,
 dm
dm
 0.26,
0.26,


 0.70, and
a Hubble constant
h
0.70, and
a Hubble constant
h  0.7. The
spatial geometry is very close to
flat (and often assumed to be precisely flat), and the initial
perturbations Gaussian, adiabatic, and nearly scale-invariant.
0.7. The
spatial geometry is very close to
flat (and often assumed to be precisely flat), and the initial
perturbations Gaussian, adiabatic, and nearly scale-invariant.
The most powerful single experiment is WMAP, which on its own supports
all these main tenets. Values for some parameters, as given in
Spergel et al. [7],
are reproduced in Table 2. This
model presumes a flat Universe, and so

 is
a derived quantity in this analysis, with best-fit value
is
a derived quantity in this analysis, with best-fit value

 =
0.73.
=
0.73.
| WMAP alone | WMAPext + 2dFGRS | WMAPext + 2dFGRS | |
| power-law | power-law | running | |
 m
h2 m
h2 |
0.14 ± 0.02 | 0.134 ± 0.006 | 0.136 ± 0.009 |
 b
h2 b
h2 |
0.024 ± 0.001 | 0.023 ± 0.001 | 0.022 ± 0.001 |
| h | 0.72 ± 0.05 | 0.73 ± 0.03 | 0.71 ± 0.04 |
| n | 0.99 ± 0.04 | 0.97 ± 0.03 | 0.93+0.04-0.05 |
 |
0.17+0.08-0.07 | 0.15 ± 0.07 | 0.17 ± 0.06 |
| A | 0.9 ± 0.1 | 0.8 ± 0.1 | 0.84 ± 0.09 |
| dn / d ln k | - | - | -0.031+0.023-0.025 |
However, to obtain the most powerful constraints, other data sets need to be considered in addition to WMAP. A standard data compilation unites WMAP with shorter-scale CMB measurements from CBI and ACBAR, and the galaxy power spectrum from the 2dF survey. In our opinion, this combination of datasets offers the most reliable set of constraints at present. In addition, it is possible to add the Lyman-alpha forest power spectrum data, but this has proven more controversial as the interpretation of such data has not reached a secure level.
Using the extended data set without the Lyman-alpha constraints produces no surprises; as compared to WMAP alone, the best-fit values move around a little within the uncertainties, and the error bars improve somewhat, as seen in Table 2. In this table we also show the effect of allowing the spectral index to vary with scale (`running'): the running is found to be consistent with zero and there are small drifts in the values and uncertainties of the other parameters. 7
However, inclusion of the Lyman-alpha data suggests a more radical development, with the running weakly detected at around 95% confidence, the spectral index making a transition from n > 1 on large scales to n < 1 on small scales [7, 6]. The significance of this measurement is not high, and the result rather unexpected on theoretical grounds (it suggests that the power spectrum has a maximum which just happens to lie in the rather narrow range of scales that observations are able to probe, and the running is much larger than in typical inflation models giving a spectral index close to one). In our view it is premature to read much significance into this observation, though if true, it should rapidly be firmed up by new data.
The baryon density
 b is now
measured with quite high accuracy from the
CMB and large-scale structure, and shows reasonable agreement with the
determination from big bang nucleosynthesis; Fields and Sarkar in this
volume quote the range
0.012
b is now
measured with quite high accuracy from the
CMB and large-scale structure, and shows reasonable agreement with the
determination from big bang nucleosynthesis; Fields and Sarkar in this
volume quote the range
0.012 
 b
h2
b
h2  0.025. Given the sensitivity of the
measurement, it is important to note that it has significant dependence
on both the datasets and parameter sets chosen, as seen in
Table 2.
0.025. Given the sensitivity of the
measurement, it is important to note that it has significant dependence
on both the datasets and parameter sets chosen, as seen in
Table 2.
While 
 is
measured to be non-zero with very high
confidence, there is no evidence of evolution of the dark energy
density. The WMAP team find
the limit w < - 0.78 at 95% confidence from a compilation of
data including SNe Ia data, where they impose a prior w
is
measured to be non-zero with very high
confidence, there is no evidence of evolution of the dark energy
density. The WMAP team find
the limit w < - 0.78 at 95% confidence from a compilation of
data including SNe Ia data, where they impose a prior w
 - 1, with the cosmological
constant case w = - 1 giving an excellent fit to the data.
- 1, with the cosmological
constant case w = - 1 giving an excellent fit to the data.
As far as inflation is concerned, the data provide good news and bad
news. The
good news is that WMAP supports all the main predictions of the simplest
inflation models: spatial flatness and adiabatic, Gaussian, nearly
scale-invariant density perturbations. But it is disappointing that
there is no sign of primordial gravitational waves, with WMAP providing
only a weak upper limit r < 0.53 at 95% confidence
[6]
(this assumes no running,
and weakens significantly if running is allowed), and especially that no
convincing deviations from scale-invariance have been seen. It is
perfectly possible for inflation models to give
n  1 and r
1 and r
 0, but in that limit, the
observations give no clues as to the dynamical processes driving inflation.
Tests have been made for various types of non-Gaussianity, a particular
example being a parameter fNL which measures a quadratic
contribution to the perturbations and is constrained to
-58 < fNL < 134 at 95%
confidence [41]
(this looks weak, but prominent non-Gaussianity
requires the product fNL
0, but in that limit, the
observations give no clues as to the dynamical processes driving inflation.
Tests have been made for various types of non-Gaussianity, a particular
example being a parameter fNL which measures a quadratic
contribution to the perturbations and is constrained to
-58 < fNL < 134 at 95%
confidence [41]
(this looks weak, but prominent non-Gaussianity
requires the product fNL
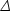
 to be large,
and
to be large,
and
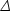
 is of order
10-5).
is of order
10-5).
Two parameters which are still uncertain are
 m and
m and
 8 (see
Figure 4
and Ref. [42]).
The value of
8 (see
Figure 4
and Ref. [42]).
The value of
 m is
beginning to be pinned down with some
precision, with most observations indicating a value around 0.3,
including the CMB anisotropies, the cluster number density, and
gravitational lensing, though the latter two have a strong degeneracy
with the amplitude of mass fluctuations
m is
beginning to be pinned down with some
precision, with most observations indicating a value around 0.3,
including the CMB anisotropies, the cluster number density, and
gravitational lensing, though the latter two have a strong degeneracy
with the amplitude of mass fluctuations
 8. However,
not all observations
yet agree fully on this, for instance mass-to-light ratio measurements give
8. However,
not all observations
yet agree fully on this, for instance mass-to-light ratio measurements give
 m
m
 0.15
[43],
and the fractional
uncertainty remains significantly higher than one would like. Concerning
0.15
[43],
and the fractional
uncertainty remains significantly higher than one would like. Concerning
 8, results
from the cluster number density have varied quite a lot in recent years,
spanning the range 0.6 to 1.0, primarily due to the uncertainties
in the mass-temperature-luminosity relations used to connect the
observables with theory.
There is certainly scope for improving this calibration by comparison
to mass measurements from strong gravitational lensing.
The WMAP-alone measurements gives
8, results
from the cluster number density have varied quite a lot in recent years,
spanning the range 0.6 to 1.0, primarily due to the uncertainties
in the mass-temperature-luminosity relations used to connect the
observables with theory.
There is certainly scope for improving this calibration by comparison
to mass measurements from strong gravitational lensing.
The WMAP-alone measurements gives
 8 = 0.9
± 0.1. However, this is not a direct
constraint; WMAP only probes larger length scales, and the constraint
comes from using WMAP to estimate all the parameters of the model needed to
determine
8 = 0.9
± 0.1. However, this is not a direct
constraint; WMAP only probes larger length scales, and the constraint
comes from using WMAP to estimate all the parameters of the model needed to
determine  8.
As such, their constraint depends strongly on the
assumed set of cosmological parameters being sufficient.
8.
As such, their constraint depends strongly on the
assumed set of cosmological parameters being sufficient.
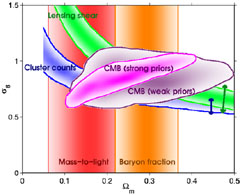 |
Figure 4. Various constraints shown in the
|
One parameter which is surprisingly robust is the age of the Universe. There is a useful coincidence that for a flat Universe the position of the first peak is strongly correlated with the age of the Universe. The WMAP-only result is 13.4 ± 0.3 Gyr (assuming a flat Universe). This is in good agreement with the ages of the oldest globular clusters [44] and radioactive dating [45].
7 As we were finalizing this article, an analysis of WMAP combined with the SDSS galaxy power spectrum appeared [40], giving results in good agreement with those discussed here. Back.