The observed prompt emission must be generated by energetic particles that have been accelerated within the collisionless shocks. The most likely process is synchrotron emission, even though there is some evidence that a simple synchrotron spectra does not fit all bursts [321] (but see however, [16] who finds consistency with the synchrotron model). I consider here, the different physical ingredient that determine the emission process: particle acceleration, magnetic field amplification, synchrotron emission and inverse Compton emission that could be relevant in some cases.
Shocks involve sharp jumps in the physical conditions. Conservation of mass, energy and momentum determine the Hugoniot shock jump conditions across the relativistic shocks for the case when the upstream matter is cold (see e.g. Blandford and McKee [30]):
 |
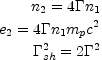(10) |
where n1, 2,e1, 2 are the number
density and the energy
density (measured in the local rest frame) of the matter upstream
(region 1) and downstream (region 2). I have assumed that the
energy density in region 1 is very small compared to the rest mass
density. 
is the
Lorentz factor of the fluid just behind the shock and
sh is the
Lorentz factor of the shock front
(both measured in the rest frame of the upstream fluid). The
matter is compressed by a factor
across a relativistic
shock. The pressure, or the internal energy density behind the
shock is of order
2
n1 mp c2. Thus, in
the shock's rest frame the relative "thermal" energy per particle
(downstream) is of the same order of the kinetic energy per
particle (ahead of the shock) upstream. Put differently the shock
converts the `ordered' kinetic energy to a comparable random
kinetic energy. In an ultra-relativistic shock the downstream
random velocities are ultra-relativistic.
Similar jump conditions can be derived for the Magnetic fields across the shock. The parallel magnetic field (parallel to the shock front) B|| is compressed and amplified:
 |
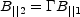(11) |
The perpendicular magnetic field
B
remains unchanged.
The energy distribution of the (relativistic) electrons and the
magnetic field behind the shock are needed to calculate the
Synchrotron spectrum. In principle these parameters should be
determined from the microscopic physical processes that take place
in the shocks. However, it is difficult to estimate them from
first principles. Instead I define two dimensionless parameters,
B and
e, that
incorporate our ignorance and uncertainties
[288,
305,
367].
It is commonly assumed
that these energies are a constant fraction of the internal energy
behind the shock (see however, Daigne and Mochkovitch
[68]).
I denote by
e and by
B the
ratio between these energies and the total internal energy:
 |
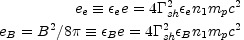(12) |
One usually assumes that these factors,
e,B, are
constant through out the burst evolution. One may even expect
that they should be constant from one burst to another (as they
reflect similar underlying physical processes). However, it seems
that a simple model that assumes that these parameters are
constant during the prompt burst cannot reproduce the observed
spectrum [68].
This leads to explorations of models in which the equipartition parameters
e,B
depend on the physical conditions within the matter.
In GRBs, as well as in SNRs the shocks are collisionless. The densities are so small so that mean free path of the particles for collisions is larger than the typical size of the system. However, one expects that ordered or random magnetic fields or alternatively plasma waves will replace in these shocks the role of particle collisions. One can generally use in these cases the Larmour radius as a typical shock width. A remarkable feature of the above shock jump conditions is that as they arise from general conservation laws they are independent of the detailed conditions within the shocks and hence are expected to hold within collisionless shocks as well. See however [263] for a discussion of the conditions for collisionless shocks in GRBs.