B. Internal Shocks

1. Hydrodynamics of Internal Shocks

Internal shocks take place when a faster shell catches a slower one, namely at:

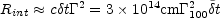(42)

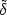where ₁₀₀ is the typical Lorentz factor in units of 10² and t is the time difference between the emission of the two shells. I show later that 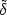t defined here is roughly equal to the observed fluctuations in the light curve of the burst t. Clearly R_int < R_ext must hold otherwise internal shocks won't take place. R_ext is defined as the location of efficient extraction of energy by external shocks (see Section VIC). If follows from the discussion in Section VIC that the condition R_int < R_ext implies:

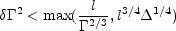(43)

where l is defined by Eq. 58 and it is typically of the order of 10¹⁸cm, while is the width of the shell and it is of order 10¹²cm. Both conditions set upper limits on (of the order of a few thousands) for internal shocks. If the initial Lorentz factor is too large then internal shocks will take place at large radii and external shocks will take place before the internal shocks could take place. It is possible that this fact plays an important role in limiting the relevant Lorentz factors and hence the range of variability of E_p, the peak energy observed in GRBs.

Internal shocks are characterized by a comparable Lorentz factor of order of a few (1 < < 10) reflecting the relative motion of the shells and by comparable densities n in both shells. In this case, for an adiabatic index (4/3), the Loretz factor of the shocked region 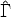satisfies:

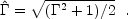(44)

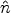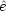The shocked density and energy are:

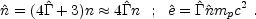(45)

Both shocks are mildly relativistic and their strength depends on the relative Lorentz factors of the two shells.

2. The Efficiency of Internal Shocks

Consider collision between two shells with masses m_r and m_s that are moving at different relativistic velocities: _{r s} >> 1. The resulting bulk Lorentz factor, _m in an elastic collision is:

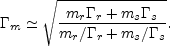(46)

The internal energy, _int, in the local frame and E_int, in the frame of an external observer, of the merged shell: E_int = _{m int}, is the difference of the kinetic energies before and after the collision:

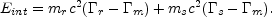(47)

The conversion efficiency of kinetic energy into internal energy is [193]:

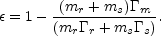(48)

As can be expected a conversion of a significant fraction of the initial kinetic energy to internal energy requires that the difference in velocities between the shells will be significant: _r >> _s and that the two masses will be comparable m_r m_s [67, 193].

Beloborodov [19] considered internal shocks between shells with a lognormal distribution of ( - 1) / (₀ - 1), where ₀ is the average Lorentz factor. The dimensionless parameter, A, measures the width of the distribution. He shows that the efficiency increases and reached unity when A is of order unity, that is typical fluctuation in are by a factor of 10 compared to the average. Similarly numerical simulations of Guetta et al. [154] show that a significant fraction of the wind kinetic energy, on the order of 20%, can be converted to radiation, provided the distribution of Lorentz factors within the wind has a large variance and the minimum Lorentz factor is greater than 10^2.5 L^2/9₅₂, where L₅₂ is the (isotropic) wind luminosity in units of 10⁵² ergs/sec.

Another problem that involves the efficiency of GRBs is that not all the internal energy generated is emitted. This depends further on _e, the fraction of energy given to the electron. If this fraction is small and if there is no strong coupling between the electrons and the protons the thermal energy of the shocked particles (which is stored in this case mostly in the protons) will not be radiated away. Instead it will be converted again to kinetic energy by adiabatic cooling. Kobayashi and Sari [195] consider a more elaborated model in which colliding shells that do not emit all their internal energy are reflected from each other, causing subsequent collisions and thereby allowing more energy to be emitted. In this case more energy is eventually emitted than what would have been emitted if we considered only the first collision. They obtain about 60% overall efficiency even if the fraction of energy that goes to electrons is small _e = 0.1. This is provided that the shells' Lorentz factor varies between 10 and 10⁴.

3. Light Curves from Internal Shocks

Both the similarity between the pulse width and the pulse separation distribution and the correlation between intervals and the subsequent pulses [270, 327] arise naturally within the internal shocks model [268]. In this model both the pulse duration and the separation between the pulses are determined by the same parameter - the interval between the emitted shells. I outline here the main argument (see Nakar and Piran [268] for details). Consider two shells with a separation L. The Lorentz factor of the slower outer shell is _S = and of the Lorentz factor inner faster shell is _F = a (a > 2 for an efficient collision). Both are measured in the observer frame. The shells are ejected at t₁ and t₂ t₁ + L / c. The collision takes place at a radius R_s 2² L (Note that R_s does not depend on ²). The emitted photons from the collision will reach the observer at time (omitting the photons flight time, and assuming transparent shells):

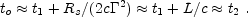(49)

The photons from this pulse are observed almost simultaneously with a (hypothetical) photon that was emitted from the "inner engine" together with the second shell (at t₂). This explains why various numerical simulations [67, 193, 293] find that for internal shocks the observed light curve replicates the temporal activity of the source.

In order to determine the time between the bursts we should consider multiple collisions. It turns out that there are just three types of collisions, (i), (ii) and (iii), that characterize the system and all combinations of multiple collisions can be divided to these three types. Consider four shells emitted at times t_i (i = 1, 2, 3, 4) with a separation of the order of L between them. In type (i) there are two collisions - between the first and the second shells and between the third and the fourth shells. The first collision will be observed at t₂ while the second one will be observed at t₄. Therefore, t t₄ - t₂ 2L / c. A different collision scenario (ii) occurs if the second and the first shells collide, and afterward the third shell takes over and collide with them (the forth shell does not play any roll in this case). The first collision will be observed at t₂ while the second one will be observed at t₃. Therefore, t t₃ - t₂ L / c. Numerical simulations [268] show that more then 80% of the efficient collisions follows one of these two scenarios ((i) or (ii)). Therefore one can estimate:

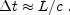(50)

Note that this result is independent of the shells' masses.

A third type of a multiple collision (iii) arises if the third shell collides first with the second shell. Then the merged shell will collide with the first one (again the fourth shell does not participate in this scenario). In this case the two pulses merge and will arrive almost simultaneously, at the same time with a (hypothetical) photon that would have been emitted from the inner engine simultaneously with the third (fastest) shell. t ~ t₃. Only a 20% fraction exhibits this type of collision.

The pulse width is determined by the angular time (ignoring the cooling time): t = R_s / (2c _s²) where _s is the Lorentz factor of the shocked emitting region. If the shells have an equal mass (m₁ = m₂) then _s = a while if they have equal energy (m₁ = a m₂) then _s . Therefore:

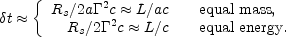(51)

The ratio of the Lorentz factors a, determines the collision's efficiency. For efficient collision the variations in the shells Lorentz factor (and therefore a) must be large.

It follows from Eqs. 50 and 51 that for equal energy shells the t - t similarity and correlation arises naturally from the reflection of the shells initial separation in both variables. However, for equal mass shells t is shorter by a factor of a than t. This shortens the pulses relative to the intervals. Additionally, the large variance of a would wipe off the t - t correlation. This suggests that equal energy shells are more likely to produce the observed light curves.