L. Generalizations: VI. Additional Physical Processes

With the development of the theory of GRB afterglow it was realized that several additional physical ingredients may influence the observed afterglow light emission. In this section I will review two such processes: (i) Pre acceleration of teh surrounding matter by the prompt -rays emission and (ii) Decay of neutrons within the outflow.

1. Pre-acceleration

The surrounding regular ISM or even stellar wind is optically thin to the initial -rays pulse. Still the interaction of the pulse and the surrounding matter may not be trivial. Thompson and Madau [407] pointed out that a small fraction of the -rays radiation will be Compton scattered on the surrounding electrons. The backscattered photons could now interact with the outwards going -rays flux and produce pairs. The pairs will increase the rate of backscattering and this could lead to an instability. When sufficient number of pairs will be produced the surrounding matter will feel a significant drag by the -rays flux and it will be accelerated outwards [244]. These pre-acceleration of the ambient medium could have several implications to the early afterglow [21, 233].

The key issue is that while the optical depth of the surrounding medium (as "seen" the -rays photons) is very small, the mean free path of an ambient electron within the -rays photons is large (at small enough radius) and each electron scatters many photons. While the medium absorbs only a small fraction of the prompt -rays energy, the effect of this energy can be significant. Beloborodov [20] characterizes the interaction of the -rays radiation front with the surrounding medium by a dimensionless parameter ¹¹:

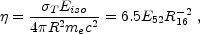(114)

the energy that a single electron scatters relative to its rest mass. Beloborodov [21] calculates the Lorentz factor of the ambient medium and the number of pairs per initial electron as functions of , where _load = 20 - 30, depending on the spectrum of the gamma-rays, _acc = 5_load = 100 - 150, and f_acc = [exp(_acc / _load) + exp(- _acc / _load)]/2 = 74.

If < _load 20 - 30, depending on the spectrum of the gamma-rays, the medium remains static and e^±-free. When the front has > _load, a runaway e^± loading occurs. The number of loaded pairs depends exponentially on as long as < _acc = 5_load = 100 - 150. The medium is accelerated if > _acc. _acc is around 100 because the electrons are coupled to the ambient ions, and and the other hand the loaded e^± increase the number of scatters per ion. At = _gap 3 × 10³, the matter is accelerated to a Lorentz factor _ambient that exceeds the Lorentz factor of the ejecta. It implies that the radiation front pushes the medium away from the ejecta and opens a gap.

As the GRB radiation front expands, the energy flux and hence decreases R^-2. passes through _gap, _acc, and _load at R_gap, R_acc, and R_load, respectively. These three characteristic radii define four stages:

i. R < R_gap R_acc / 3: The ejecta moves in a cavity produced by the radiation front with _ambient > _ejecta.

II. R_gap < R < R_acc 3 × 10¹⁵ cm E₅₂^1/2 cm: The ejecta sweeps the e^±-rich medium that has been preaccelerated to 1 << _ambient < _ejecta.

III. R_acc < R < R_load 2.3R_acc. The ejecta sweeps the "static" medium (_ambient 1) which is still dominated by loaded e^±.

IV. R > R_load. The ejecta sweeps the static pair-free medium.

This influence of the -rays ;on the surrounding matter may modify the standard picture of interaction of external shocks with the surrounding medium (see Section VIC1. This depends mostly on the relation between R_ext and R_gap 10¹⁵ E₅₂^1/2 cm. If R_ext > R_gap this effect won't be important. However, if R_ext < R_gap then effective decceleration will begin only at R_gap. At R < R_gap the ejecta freely moves in a cavity cleared by the radiation front and only at R = R_gap the blast wave gently begins to sweep the preaccelerated medium with a small relative Lorentz factor. With increasing R > R_gap, _ambient falls off quickly, and it approaches _ambient = 1 at R = R_acc 3R_gap as _ambient = (R / R_acc)^-6. Thus, after a delay, the ejecta suddenly "learns" that there is a substantial amount of ambient material on its way. This resembles a collision with a wall and results in a sharp pulse (see Fig. 33).

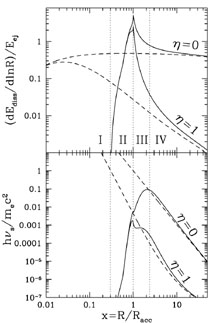Figure 33. Afterglow from a GRB ejecta decelerating in a wind of a Wolf-Rayet progenitor with = 2 × 10-5 M yr-1 and w = 103 km s-1. The burst has an isotropic energy E = 1053 erg) and a thin ejecta shell with kinetic energy E = 1053 erg and a Lorentz factor = 200. Dashed curves show the prediction of the standard model that neglects the impact of the radiation front, and solid curves show the actual behavior. Two extreme cases are displayed in the figure: = 0 (adiabatic blast wave) and = 1 (radiative blast wave). Four zones are marked: I - R < Rgap (the gap is opened), II - Rgap < R < Racc (the gap is closed and the ejecta sweeps the relativistically preaccelerated e±-loaded ambient medium), III - Racc < R < Rload (e±-loaded ambient medium with ambient 1), and IV - R > Rload (pair-free ambient medium with ambient 1). The radie are measured in units of Racc 1016 cm. Top panel: dissipation rate. Bottom panel: synchrotron peak frequency (assuming B = 0.1) in units of me c2 / h. From Beloborodov [20].

While R_gap does not depend on the external density R_ext does (see Eq. 65). The condition R_ext < R_gap implies:

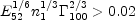(115)

Thus it requires a dense external medium and large initial Lorentz factor. Otherwise R_gap is too large and the deceleration takes place after the gap is closed. Hence the conditions for pre-acceleration will generally occur if the burst takes place in a dense circumburst regions, like in a Wolf-Rayet progenitor [21]. Kumar and Panatescu [205] elaborate on this model and find that the observational limits by LOTIS and ROTSE on prompt emission from various burst limit the ambient ISM density (within 10¹⁶cm to less than 10³ cm^-3. Similarly the find that in case of a wind the progenitors mass loss to wind's velocity ratio is below 10^-6 M / yr / (10³ km/sec).

2. Neutron decoupling and decay

Derishev et al. [75, 76] pointed out that neutrons that are included initially in the fireball will change its dynamics and modify the standard afterglow evolution. While the protons slow down due to the interaction with the surrounding matter the neutrons will coast freely after they decouple with _n, which equals to the Lorentz factor while decoupling took place.

At

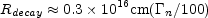(116)

the neutrons decay. A new baryonic shell forms ahead of the original fireball shell, with energy comparable to the initial energy of the protons' shell (this depends, of course, on the initial ratio of neutrons to protons). At this stage the neutrons front that is not slowed down like the rest of the fireball is at a distance:

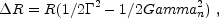(117)

from the fireball front, where is the current Lorentz factor of the fireball.

Once more the situation depends on whether R_decay is smaller or larger than R_ext, the original deceleration radius. If R_decay < R_ext:

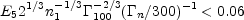(118)

the decaying neutron products will mix with the original protons and won't influence the evolution significantly (apart from adding their energy to the adiabatic fireball energy). Otherwise, they situation depends on _n the Lorentz factor at decoupling.

Pruet and Dalal [325] consider a situation in which the neutron decouple with a low _n. In this case one will get a delayed shock scenario when the neutronic decay produce will eventually catch up with the slowing down protons (when their Lorentz factor is of order _n. Along the same line of thought Dalal et al. [69] suggest that a large neutronic component that may exist within the initial fireball material may help to eliminate the baryon load problem [385].

Beloboradov [22] considers a situation when _{n 0}, the initial Lorentz factor of the protons. In this case the decaying neutrons' products will be ahead of the shell of the protons. The decaying products will interact with the surrounding matter and will begin to slow down. There will be a triple interaction between the two shells and the surrounding ambient medium (resembling to some extend the pre-acceleration scenario described earlier) . This will take place at radii of a few times R_decay and at an observed time of a few × R_decay / 2c ² a fews econds / (_n / 300), i.e. extremely early. This will produce brightening when the fronts pass R_decay.

The neutrons could also influence the behavior of the relativistic flow during the prompt (internal shocks) phase. Specifically inelastic collisions between differentially streaming protons and neutrons can produce pions and eventually _µ of 10 GeV as well as _e of 5 GeV [12, 238]. These neutrino fluxes could produce ~ 7 events/year in km3 neutrino detectors. GeV photons will also be produced but it is unlikely that they could be detected.

¹¹ Note that Beloborodov [20] uses the notation for this parameter. Back.