D. Gravitational Radiation

Like GRBs, typical sources of gravitational radiation involve the formation of compact objects. Hence it is reasonable to expect that gravitational waves will accompany GRBs. This association is indirect: the gravitational waves are not directly related to the GRB. Additinionally, GRBs have their own, albeit weak, gravitational radiation pulse which arises during the acceleration of the jets to relativistic velocities. Unfortunately this signal is weak and moreover it is perpendicular to the GRB signal.

To estimate the rates of observed gravitational radiation events associated with GRB we use the rate of long GRBs. The nearest (long) GRB detected within a year would be at 1 Gpc. As GRBs are beamed the nearest (long) event would be at would be much nearer, at 135 _0.1² Mpc. However, this burst would be directed away from us. Still a GRB that is beamed away from us is expected to produce an "orphan" afterglow.

The rate of short bursts is less certain. Schmidt [381] estimates that the rate of short GRBs is smaller by a factor of two than the rate of long ones. In this case the distances mentioned above should be revised up by a factor of 1.25. However, if the rate of short GRBs is larger by a factor 10 than the rate of long ones then the corresponding distances should be revised downwards by a factor of 10^-1/3 This would put one event per year at ~ 80 _0.1² Mpc, but once again this burst won't be pointing towards us. The nearest event with a burst in our direction would be at ~ 450 Mpc.

1. Gravitational Radiation from Neutron Star Mergers

Binary neutron star mergers are the "canonical" sources of gravitational radiation emission. LIGO and VIRGO both aim in detecting these sources. Specifically the goal of these detectors is to detect the characteristic "chirping" signals arising from the in-spiraling phase of these events. The possibility of detection of such signals has been extensively discussed (see e.g. [63]). Such events could be detected up to a distance of several tens of Mpc with LIGO I and up to ~ 100 Mpc with LIGO II.

Comparing with GRB rates we find that if, as some expect, neutron star mergers are associated with short GRBs and if the rate of short GRBs is indeed large, then we have one event per year within the sensitivity of LIGO II and marginally detectable by LIGO I. However, this burst will be pointing away from us.

The detection of the chirping merger signal is based on fitting the gravitational radiation signal to pre-calculated templets. Kochaneck and Piran [196] suggested that the detection of a merger gravitational radiation signal would require a lower S/N ratio if this signal coincides with a GRB. This would increase somewhat the effective sensitivity of LIGO and VIRGO to such events. Finn et al. [97] suggest using the association of GRBs with sources of gravitational waves in a statistical manner and propose to search for enhanced gravitational radiation activity towards the direction of a GRB during the short periods when GRBs are detected. Given the huge distances of observed GRBs it is not clear if any of these techniques will be useful.

2. Gravitational Radiation from Collapsars

The Collapsar model [242, 287, 443] is based on the collapse of the core of a massive star to a black hole surrounded by a thick massive accretion disk. As far as gravitational radiation is concerned this system is very similar to a regular supernova. Rotating gravitational collapse has been analyzed by Stark and Piran [397]. They find that the gravitational radiation emission emitted in a rotating collapse to a black hole is dominated by the black hole's lowest normal modes, with a typical frequency of 20c³ / GM. The total energy emitted is:

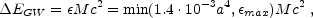(119)

where a is the dimensionaless specific angular momentum and _max is a maximal efficiency which is of the order a few × 10^-4. The expected amplitude of the gravitational radiation signal, h, would be of the order of ^1/2 GM / c²d where d is the distance to the source. Even LIGO II won't be sensitive enough to detect such a signal from a distance of 1Gpc or even from 100 Mpc.

3. Gravitational Radiation from Supranova

According to the Supranova model a GRB arises after a neurton star collapse to a black hole. This collapse takes PLACE several weeks or months after the Supernova that formed the neutron star (see IXE). The expected gravitational waves signal from a Supranova [426] includes two components. First the signal from the initial supernova is similar to the gravtitational waves from the collapsar model. However, here the first collapse (the Supernova) takes place several weeks or months before the GRB. Thus, there won't be any correlation between the gravitational waves emitted by the first collapse and the GRB. A second component may arise from the second collapse from the supramassive neutron star to a black hole. This signal should coincide with the GRB.

4. Gravitational Radiation from the GRB

The most efficient generation of gravitational radiation could take place here during the acceleration phase, in which the mass is accelerated to a Lorentz factor . To estimate this emission I follow Weinberg [437] analysis of gravitational radiation emitted from a relativistic collision between two particles. Consider the following simple toy model: two particles at rest with a mass M that are accelerated instantly at t = 0 to a Lorentz factor and energy E. Conservation of energy requires that some (actually most) of the rest mass is converted to kinetic energy during the acceleration and the rest mass of the accelerated particle is m = E / = M / . The energy emitted per unit frequency per unit solid angle in the direction at an angle relative to is:

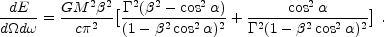(120)

The result is independent of the frequency, implying that the integral over all frequency will diverge. This nonphysical divergence arises from the nonphysical assumption that the acceleration is instantaneous. In reality this acceleration takes place over a time t, which is of order 0.01 sec. This would produce a cutoff _max ~ 2 / t above which Eq. 120 is not valid. The angular distribution found in Eq. 120 is disappointing. The EM emission from the ultrarelativistic source is beamed forwards into a small angle 1/, enhancing the emission in the forwards direction by a large factor (²). The gravitational radiation from this relativistic ejecta is spread rather uniformly in almost all 4 steradians. Instead of beaming there is "anti-beaming" with no radiation at all emitted within the forward angle 1/ along the direction of the relativistic motion.

Integration of the energy flux over different directions yields:

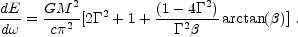(121)

As expected the total energy emitted is proportional to m^{2 2}. Further integration over frequencies up to the cutoff 2 / t yields:

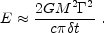(122)

In reality the situation is much more complicated than the one presented here. First, the angular width of the emitted blobs is larger than 1 / . The superposition of emission from different directions washes out the no emission effect in the forward direction. Additionally according to the internal shocks model the acceleration of different blobs go on independently. Emission from different blobs should be combined to get the actual emission. Both effects reduce the effective emission of gravitational radiation and makes the above estimate an upper limit to the actual emission.

The gravitational signal is spread in all directions (apart from a narrow beam along the direction of the relativistic motion of the GRB). It ranges in frequency from 0 to f_max 100 Hz. The amplitude of the gravitational radiation signal at the maximal frequency, f_max 100 Hz, would be: h (GM ² / c² d ). For typical values of E = M = 10⁵¹ ergs, t = 0.01 sec and a distance of 500 Mpc, h .5 ^. 10^-25, it is far below the sensitivity of planned gravitational radiation detectors. Even if we a burst is ten times nearer this "direct" gravitational radiation signal would still be undetectable.

Some specific models for GRBs' inner engine predict additional amount of energy. For example vanPutten [417], vanPutten and Levinson [418] suggest a model of a black hole - accretion torus in which a large fraction of the emitted energy of the black hole - accretion torus system escapes as gravitational radiation. The radiation arises due to instabilities within the torus that break down the axial symmetry. They estimate that as much as 10⁵³ ergs would be emitted as gravitational radiation which will have a characteristic signature corresponding to the normal mode of the black hole - accretion torus system with typical frequencies around few hundred Hz, conveniently within the frequency range of LIGO/VIRGO. If correct than GRBs are the most powerful burst-sources of gravitational waves in the Universe [417].