The key to understanding GRBs lies, I believe, in understanding how GRBs bypass the compactness problem. This problem was realized very early on in one form by Ruderman [205] and in another way by Schmidt [206]. Both used it to argue that GRBs cannot originate from cosmological distances. Now, we understand that GRBs are cosmological and special relativistic effects enable us to overcome this constraint.
The simplest way to see the compactness problem is to estimate the average opacity of the high energy gamma-ray to pair production. Consider a typical burst with an observed fluence, F. For a source emitting isotropically at a distance D this fluence corresponds to a total energy release of:
 |
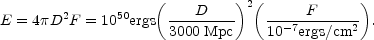(8) |
Cosmological effects change this equality by numerical factors of
order unity that are not important for our discussion. The rapid
temporal variability on a time scale
T
10 msec implies that
the sources are compact with a size,
Ri < c
T
3000 km. The observed
spectrum (see
section 2.3) contains a large fraction of high
energy 
-ray
photons. These photons (with energy E1) could
interact with lower energy photons (with energy E2)
and produce electron-positron pairs via
e+
e- if
(E1 E2)1/2 >
me c2
(up to an angular factor). Denote by fp the fraction
of photon pairs that satisfy this condition. The average optical depth
for this process is
[207,
208,
209]:
 |
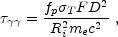or
 |
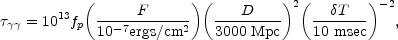(9) |
where 
T is
the Thompson cross-section. This optical depth is
very large. Even if there are no pairs to begin with they will form
rapidly and then these pairs will Compton scatter lower energy
photons, resulting in a huge optical depth for all photons. However, the
observed non-thermal spectrum indicates with certainty that the
sources must be optically thin!
An alternative calculation is to consider the optical depth of the highest energy photons (say a GeV photon) to pair production with the lower energy photons. The observation of GeV photons shows that they are able to escape freely. In other words it means that this optical depth must be much smaller than unity [210, 211]. This consideration leads to a slightly stronger but comparable limit on the opacity.
The compactness problem stems from the assumption that the size of
the sources emitting the observed radiation is determined by the
observed variability time scale. There won't be a problem
if the source emitted the energy in another form and it was converted
to the observed gamma-rays at a large distance, RX,
where the system is optically thin and
(RX) < 1. A
trivial solution of this kind is based on a weakly interacting
particle, which is converted in flight to electromagnetic radiation.
The only problem with this solution is that there is no known particle
that can play this role (see, however
[213]).