Next Contents Previous

5.3. Typical Radii

Table 3. Critical Radii (a) - adiabatic fireball; (b) - radiative fireball
Ri Initial Radius c deltat approx 107 - 108 cm
Reta Matter dominates Rieta approx 109 cm
Rpair Optically thin to pairs [(3E / 4pi Ri3 a)1/4 / Tp] Ri approx 1010 cm
Re Optically thin (sigmaT E / 4pi mp c2 eta)1/2 approx 1013 cm
Rdelta Internal collisions delta gamma2 approx 1012 - 1014 cm
Rgamma External Newtonian Shocks l gamma-2/3 approx 1016 cm
RDelta External Relativistic shocks l3/4 Delta1/4 approx 1016 cm
l or L Non relativistic external shock l (a) or lgamma-1/3 (b) approx 1017 - 1018 cm
l Sedov Length l = (3E / 4pi nism mp c2)1/3 approx 1018 cm

Figs. 12 and 13 (from [228]) depict a numerical solution of a fireball from its initial configuration at rest to its final Sedov phase.

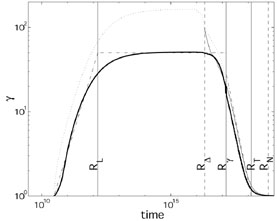Figure 12

Figure 12. Fireball evolution from its initial formation at rest to the final Newtonian Sedov solution. The energy extraction is due to the interaction with the ISM via a relativistic forward shock and a Newtonian reverse shock. We have used for this calculations xi = 43, E0 = 1052 [erg], gamma0 = 50 R0 = 3 × 1010[cm]. Shown are the average value of the Lorentz factor (thick solid line), the value at the forward shock (thin solid line), the maximal value (dotted line) and an analytic estimate (dashed dotted line). From [228].

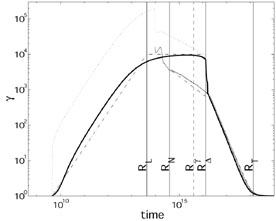Figure 13

Figure 13. Fireball evolufrom its initial formation at rest to the final Newtonian Sedov solution. The energy extraction is due to the interaction with the ISM via relativistic forward and reverse shocks. The parameters for this computation are: xi = 0.1, E0 = 1052 [erg], gamma0 = 104, R0 = 4.3 × 109 [cm]. Shown are the average value of the Lorentz factor (thick solid line), the value at the forward shock (thin solid line), the maximal value (dotted line) and an analytic estimate (dashed dotted line). From [228].

Next Contents Previous