6.3. The Radiation-Dominated Phase

Initially the fireball is radiation dominated. For << (e₀ / ₀) ₀, the first term in Eq 20 dominates and we find D r, r, recovering the radiation-dominated scaling:

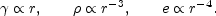(22)

The scalings of and e given in Eq. 22 correspond to those of a fluid expanding uniformly in the comoving frame. Indeed, all three scalings in Eq. 22 can be derived for a homogeneous radiation dominated fireball by noting the analogy with an expanding universe.

Although the fluid is approximately homogeneous in its own frame, because of Lorentz contraction it appears as a narrow shell in the observer frame, with a radial width given by r ~ r / ~ constant ~ R_i, the initial radius of the fireball, or the initial width of the specific shell under discussion when we consider a continuous wind. We can now go back to Eqs. 16-18 and set / s ~ / r. We then find that the terms we neglected on the right hand sides of these equations are smaller than the terms on the left by a factor ~ 1 / . Therefore, the conservation laws 19 and the scalings 22 are valid so long as the radiation-dominated fireball expands ultra-relativistically with large . The only possible exception is in the very outermost layers of the fireball where the pressure gradient may be extremely steep and / s may be >> / r. Ignoring this minor deviation, we interpret Eq. 19 and the constancy of the radial width r in the observer frame to mean that the fireball behaves like a pulse of energy with a frozen radial profile, accelerating outward at almost the speed of light.