


6.5. Spreading
At very late times in the matter-dominated phase the frozen pulse
approximation begins to break down. In this stage the radiation
density e is much smaller than the matter density
 , and the
Lorentz factor,
, and the
Lorentz factor,
 , tends to
a constant value
, tends to
a constant value
 f
for each shell. We may therefore neglect the term
- (1/3)(
f
for each shell. We may therefore neglect the term
- (1/3)( e /
e /
 r) in Eq. 18
and treat
r) in Eq. 18
and treat
 and
u in Eqs. 16-18 as constants. We then find that the flow moves
strictly along the characteristic,
and
u in Eqs. 16-18 as constants. We then find that the flow moves
strictly along the characteristic,
 f
t - r = constant, so that each fluid
shell coasts at a constant radial speed,
f
t - r = constant, so that each fluid
shell coasts at a constant radial speed,
 f
= uf /
f
= uf /
 f.
We label the baryonic shells in the fireball by a Lagrangian coordinate
f.
We label the baryonic shells in the fireball by a Lagrangian coordinate
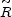 , moving with a fixed
Lorentz factor
, moving with a fixed
Lorentz factor  f(
f(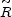 ), and let tc and rc
represent the time and radius at which the
coasting phase begins, which corresponds essentially to the point at
which the fluid makes the transition from being radiation dominated to
matter dominated. We then find
), and let tc and rc
represent the time and radius at which the
coasting phase begins, which corresponds essentially to the point at
which the fluid makes the transition from being radiation dominated to
matter dominated. We then find
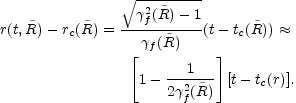 |
(24) |
The separation between two neighboring shells separated by a
Lagrangian distance 
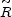 varies during the coasting
phase as
varies during the coasting
phase as
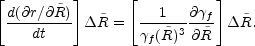 |
(25) |
Thus the width of the pulse at time t is
 r(t)
r(t)

 rc
+
rc
+ 
 f(t - tc) /
f(t - tc) /
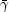 f3
f3
 Ri + (t - tc) /
Ri + (t - tc) /
 f2, where
f2, where
 rc
~ Ri
is the width of the fireball when it begins coasting,
rc
~ Ri
is the width of the fireball when it begins coasting,
 f is the mean
f is the mean
 f
in the pulse, and
f
in the pulse, and

 f
~
f
~  f is the spread of
f is the spread of
 f
across the pulse. From this result we see that
within the matter dominated coasting phase there are two separate
regimes. So long as t - tc <
f
across the pulse. From this result we see that
within the matter dominated coasting phase there are two separate
regimes. So long as t - tc <
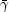 f2Ri, we have a
frozen-coasting phase in which
f2Ri, we have a
frozen-coasting phase in which
 r is
approximately constant
and the frozen pulse approximation is valid. In this regime the
scalings in Eq. 23 are satisfied. However, when
t - tc >
r is
approximately constant
and the frozen pulse approximation is valid. In this regime the
scalings in Eq. 23 are satisfied. However, when
t - tc >
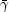 f2 Ri, the fireball
switches to an expanding-coasting phase where
f2 Ri, the fireball
switches to an expanding-coasting phase where
 r
r
 t -
tc and the pulse width grows
linearly with time. In this regime the scaling of
t -
tc and the pulse width grows
linearly with time. In this regime the scaling of
 reverts to
reverts to

 r-3, and, if the radiation is still coupled to the
matter, e
r-3, and, if the radiation is still coupled to the
matter, e  r-4.
r-4.