2. THE SUNYAEV-ZEL'DOVICH EFFECT

2.1. Thermal Sunyaev-Zel'dovich Effect

The SZE is a small spectral distortion of the CMB spectrum caused by the scattering of the CMB photons off a distribution of high-energy electrons. We only consider the SZE caused by the hot thermal distribution of electrons provided by the ICM of galaxy clusters. CMB photons passing through the center of a massive cluster have a _e 0.01 probability of interacting with an energetic ICM electron. The resulting inverse-Compton scattering preferentially boosts the energy of the CMB photon, causing a small ( 1 mK) distortion in the CMB spectrum. To illustrate the small effect, Figure 1 shows the SZE spectral distortion for a fictional cluster that is over 1000 times more massive than a typical cluster. The SZE appears as a decrease in the intensity of the CMB at frequencies below 218 GHz and as an increase at higher frequencies.

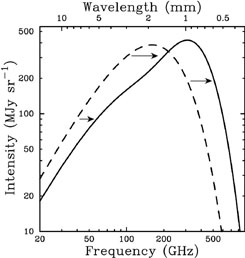Figure 1. The CMB spectrum, undistorted (dashed line) and distorted by the SZE (solid line). Following Sunyaev & Zel'dovich (1980), to illustrate the effect, the SZE distortion shown is for a fictional cluster 1000 times more massive than a typical massive galaxy cluster. The SZE causes a decrease in the CMB intensity at frequencies 218 GHz (~ 1.4 mm) and an increase at higher frequencies.

The SZE spectral distortion of the CMB, expressed as a temperature change T_SZE at dimensionless frequency x (h ) / (k_B T_CMB), is given by

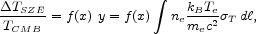(1)

where y is the Compton y-parameter, which for an isothermal cluster equals the optical depth times the fractional energy gain per scattering. Here, _T is the Thomson cross-section, n_e is the electron number density, T_e is the electron temperature, k_B is the Boltzmann's constant, m_e c² is the electron rest-mass energy, and the integration is along the line of sight. The frequency dependence of the SZE is

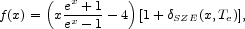(2)

where _SZE(x, T_e) is the relativistic correction to the frequency dependence. Note that f (x) -2 in the nonrelativistic and Rayleigh-Jeans (RJ) limits.

It is worth noting that T_SZE / T_CMB is independent of redshift, as shown in Equation 1. This unique feature of the SZE makes it a potentially powerful tool for investigating the high-redshift Universe.

Expressed in units of specific intensity, common in millimeter SZE observations, the thermal SZE is

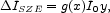(3)

where I₀ = 2(k_B T_CMB)³ / (hc)² and the frequency dependence is given by

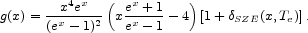(4)

T_SZE and I_SZE are simply related by the derivative of the blackbody with respect to temperature, |dB / dT|.

The spectral distortion of the CMB spectrum by the thermal SZE is shown in Figure 2 (solid line) for a realistic massive cluster (y = 10^-4), in units of intensity (left panel) and RJ brightness temperature (right panel). The RJ brightness is shown because the sensitivity of a radio telescope is calibrated in these units. It is defined simply by I = (2k_B ² / c²)T_RJ, where I is the intensity at frequency , k_B is Boltzmann's constant, and c is the speed of light. The CMB blackbody spectrum, B(T_CMB), multiplied by 0.0005 (dotted line), is also shown for comparison. Note that the spectral signature of the thermal effect is distinguished readily from a simple temperature fluctuation of the CMB. The kinetic SZE distortion is shown by the dashed curve (Section 2.2). In the nonrelativistic regime, it is indistinguishable from a CMB temperature fluctuation.

Figure 2. Spectral distortion of the CMB radiation due to the SZE. The top panel shows the intensity, and the bottom panel shows the Rayleigh-Jeans brightness temperature. The thick solid line is the thermal SZE, and the dashed line is the kinetic SZE. For reference the 2.7 K thermal spectrum for the CMB intensity, scaled by 0.0005, is shown by the dotted line in the left panel. The cluster properties used to calculate the spectra are an electron temperature of 10 keV, a Compton y-parameter of 10-4, and a peculiar velocity of 500 km s-1.

The gas temperatures measured in massive galaxy clusters are around k_B T_e 10 keV (Mushotzky & Scharf, 1997; Allen & Fabian, 1998) and are measured to be as high as ~ 17 keV in the galaxy cluster 1E 0657 - 56 (Tucker et al., 1998). At these temperatures, electron velocities are becoming relativistic, and small corrections are required for accurate interpretation of the SZE. There has been considerable theoretical work to include relativistic corrections to the SZE (Rephaeli & Yankovitch, 1997; Molnar & Birkinshaw, 1999; Challinor & Lasenby, 1998; Challinor & Lasenby, 1999; Itoh et al., 1998; Fabbri, 1981; Wright, 1979; Dolgov et al., 2001; Nozawa et al., 1998b; Rephaeli, 1995; Sazonov & Sunyaev, 1998a; Stebbins, 1997; Sazonov & Sunyaev, 1998b). All of these derivations agree for k_B T_e 15 keV, appropriate for galaxy clusters. For a massive cluster with k_BT_e 10 keV (k_B T_e / m_e c² 0.02), the relativistic corrections to the SZE are of order a few percent in the RJ portion of the spectrum, but can be substantial near the null of the thermal effect. Convenient analytical approximations to fifth order in k_B T_e / m_e c² are presented in Itoh et al. (1998).

The measured SZE spectrum of Abell 2163, spanning the decrement and increment with data obtained from different telescopes and techniques, is shown in Figure 3 (LaRoque et al., 2003; Holzapfel et al., 1997a; Désert et al., 1998). Also plotted is the best-fit model (solid) consisting of thermal (dashed) and kinetic (dotted) SZE components. The SZE spectrum is a good fit to the data, demonstrating the consistency and robustness of modern SZE measurements.

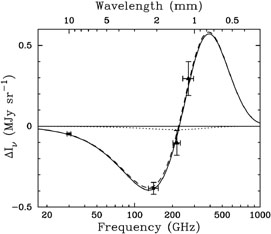Figure 3. The measured SZE spectrum of Abell 2163. The data point at 30 GHz is from BIMA (LaRoque et al., 2003), at 140 GHz is the weighted average of Diabolo and SuZIE measurements (filled square; Holzapfel et al. 1997a; Désert et al. 1998), and at 218 GHz and 270 GHz from SuZIE (filled triangles; Holzapfel et al. 1997a). Uncertainties are at 68% confidence with the FWHM of the observing bands shown. The best-fit thermal and kinetic SZE spectra are shown by the dashed line and the dotted lines, respectively, with the spectra of the combined effect shown by the solid line. The limits on the Compton y-parameter and the peculiar velocity are y0 = 3.71+0.36+0.33-0.36-0.16 × 10-4 and p = 320+880+480-740-440 km s-1, respectively, with statistical followed by systematic uncertainties at 68% confidence (LaRoque et al., 2003; Holzapfel et al., 1997a).