4. THE COSMIC DISTANCE SCALE FROM SZE/X-RAY DISTANCES

Several years after the SZE was first proposed (Sunyaev & Zel'dovich, 1972; Sunyaev & Zel'dovich, 1970) it was recognized that the distance to a cluster could be determined with a measure of its SZE and X-ray emission (Birkinshaw, 1979; Cavaliere et al., 1977; Cavaliere & Fusco-Femiano, 1978; Boynton & Murray, 1978; Gunn et al., 1978; Silk & White, 1978). The distance is determined by exploiting the different density dependences of the SZE and X-ray emissions. The SZE is proportional to the first power of the density; T_SZE ~ d n_e T_e, where n_e is the electron density, T_e is the electron temperature, and d is along the line-of-sight. The distance dependence is made explicit with the substitution d = D_A d, where D_A is the angular-diameter distance of the cluster.

The X-ray emission is proportional to the second power of the density; S_x ~ d n_e² _eH, where _eH is the X-ray cooling function. The angular-diameter distance is solved for by eliminating the electron density, ⁽³⁾ yielding

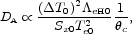(6)

where these quantities have been evaluated along the line of sight through the center of the cluster (subscript 0) and _c refers to a characteristic scale of the cluster along the line of sight, whose exact meaning depends on the density model adopted. Only the characteristic scale of the cluster in the plane of the sky is measured, so one must relate the characteristic scales along the line of sight and in the plane of the sky. For detailed treatments of this calculation, see Birkinshaw et al. (1991) and Reese et al. (2002); Reese et al. (2000). Combined with the redshift of the cluster and the geometry of the Universe, one may determine the Hubble parameter, with the inverse dependences on the observables as that of D_A. With a sample of galaxy clusters, one fits the cluster distances versus redshift to the theoretical angular-diameter distance relation, with the Hubble constant as the normalization (see, e.g., Fig. 6).

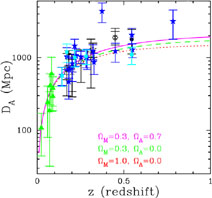Figure 6. SZE-determined distances versus redshift. The theoretical angular diameter distance relation is plotted for three different cosmologies, assuming H0 = 60 km s-1 Mpc-1: - m = 0.3, = 0.7 (solid line), open - m = 0.3 (dashed), and flat - m = 1 (dot-dashed). The clusters are beginning to trace out the angular-diameter distance relation. Three samples are highlighted: seven nearby clusters observed with the OVRO 5 m (green solid triangles; Myers et al. 1997; Mason et al. 2001); five clusters from Ryle (cyan solid squares; Grainge et al. 2002b; Jones et al. 2003; Saunders et al. 2003); and 18 clusters from the OVRO/BIMA SZE imaging project (blue solid stars; Reese et al. 2000, 2002). Additional references: Birkinshaw & Hughes 1994; Lamarre et al. 1998; Tsuboi et al. 1998; Andreani et al. 1999; Pointecouteau et al. 2001; Patel et al. 2000; Komatsu et al. 1999; Mauskopf et al. 2000; Holzapfel et al. 1997b; Birkinshaw et al. 1991; Hughes & Birkinshaw 1998.

³ Similarly, one could eliminate D_A in favor of the central density, n_e0. Back.