To set a context for the confrontation of theoretical predictions with observational data it is useful to review the physics and cosmology of the early evolution of the Universe, touching on the specifics relevant for the synthesis of the light nuclides during the first ~ 20 minutes. In this section is presented an overview of this evolution along with the predicted primordial abundances, first in the standard model and then for two examples of nonstandard models which involve variations on the early-Universe expansion rate (Steigman, Schramm, & Gunn 1977) or asymmetries between the number of neutrinos and antineutrinos (e.g., Kang & Steigman 1992, and references therein).
Discussion of BBN can begin when the Universe is a few tenths of a second old and the temperature is a few MeV. At such an early epoch the energy density is dominated by the relativistic (R) particles present, and the Universe is said to be "radiation-dominated". For sufficiently early times, when the temperature is a few times higher than the electron rest-mass energy, these are photons, e± pairs, and, for the standard model of particle physics, three flavors of left-handed (i.e. one helicity state) neutrinos (and their right-handed antineutrinos).
 |
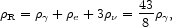(1) |
where 
is the
energy density in CBR photons (which, today, have redshifted to become
the CBR photons at a temperature of 2.7 K).
In standard BBN (SBBN) it is assumed that the neutrinos are fully
decoupled prior to e± annihilation and do not
share in the energy transferred from the annihilating
e± pairs to the CBR photons.
In this approximation, in the post-e±
annihilation Universe, the photons are hotter than the neutrinos by a
factor T /
T
=
(11/4)1/3, and the relativistic energy density is
 |
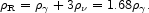(2) |
During these radiation-dominated epochs the age (t) and the energy
density are related by (32 
G / 3)
R
t2 = 1, so that once the particle content
(R)
is specified, the age of the Universe is known
(as a function of the CBR temperature
T). In the standard model,
 |
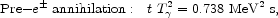(3) |
 |
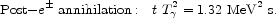(4) |
Also present at these early times are neutrons and protons, albeit in trace amounts compared to the relativistic particles. The relative abundance of neutrons and protons is determined by the charged-current weak interactions.
 |
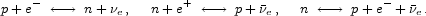(5) |
As time goes by and the Universe expands and cools, the lighter
protons are favored over the heavier neutrons and the neutron-to-proton
ratio decreases, initially following the equilibrium form
(n / p)eq
exp(- 
m /
T), where
m = 1.29 MeV
is the neutron-proton mass difference. As the temperature drops the
two-body collisions in Equation 5 become too slow
to maintain equilibrium and the neutron-to-proton ratio, while
continuing to decrease, begins to deviate from (exceeds)
this equilibrium value. For later reference, we note that if
there is an asymmetry between the numbers of
e
and 
e
("neutrino degeneracy"), described by a
chemical potential µe (such that for
µe > 0 there
are more e than
e), then
the equilibrium neutron-to-proton ratio is modified to
(n/p)
exp(- m /
T - µe / T). In place of the
neutrino chemical potential, it is convenient to introduce the
dimensionless degeneracy parameter
e
µe / T, which is invariant as the Universe
expands.
Prior to e± annihilation, at
T 
0.8 MeV when
the Universe
is ~ 1 second old, the two-body reactions regulating n/p
become slow compared to the universal expansion rate and this ratio
"freezes in", although, in reality, it continues to decrease, albeit
more slowly than would be the case for equilibrium. Later, when the
Universe is several hundred seconds old, a time comparable to the
neutron lifetime
(
n = 885.7 ±
0.8 s), the n / p ratio resumes falling exponentially:
n / p
exp(- t/n).
Since there are several billion CBR photons for every nucleon (baryon),
the abundances of any complex nuclei are entirely negligible at these
early times.
Notice that since the n / p ratio depends on the
competition between the
weak interaction rates and the early-Universe expansion rate (as well as
on a possible neutrino asymmetry), any deviations from the standard model
(e.g., R
R +
X or
e
0) will change the relative
numbers of neutrons and protons available for building more complex
nuclides.