3.1. Deuterium

The post-BBN evolution of D is straightforward. As gas is incorporated into stars the very loosely bound deuteron is burned to ³He (and beyond). Any D that passes through a star is destroyed. Furthermore, there are no astrophysical sites where D can be produced in an abundance anywhere near that observed (Epstein, Lattimer, & Schramm 1976). As a result, as the Universe evolves and gas is cycled through generations of stars, deuterium is only destroyed. Therefore, observations of the deuterium abundance anywhere, anytime, provide lower bounds on its primordial abundance. Furthermore, if D can be observed in "young" systems, in the sense of very little stellar processing, the observed abundance should be very close to the primordial value. Thus, while there are extensive data on deuterium in the solar system and the local interstellar medium of the Galaxy, it is the handful of observations of deuterium absorption in high-redshift, low-metallicity QSO absorption-line systems (QSOALS), which are potentially the most valuable. At sufficiently high redshifts and low metallicities, the primordial abundance of deuterium should reveal itself as a "deuterium plateau."

Inferring the primordial D abundance from the QSOALS has not been without its difficulties, with some abundance claims having been withdrawn or revised. Presently there are ~ half a dozen QSOALS with reasonably firm deuterium detections (Burles & Tytler 1998a, b; D'Odorico, Dessauges-Zavadsky, & Molaro 2001; O'Meara et al. 2001; Pettini & Bowen 2001; Kirkman et al. 2003). However, there is significant dispersion among the derived abundances, and the data fail to reveal the anticipated deuterium plateau (Fig. 4 - 6; see also Steigman 2003). Furthermore, subsequent observations of the D'Odorico et al. (2001) QSOALS by Levshakov et al. (2002) revealed a more complex velocity structure and led to a revised - and uncertain - deuterium abundance. This sensitivity to poorly constrained velocity structure in the absorbers is also exposed in the analyses of published QSOALS data by Levshakov and collaborators (Levshakov, Kegel, & Takahara 1998a, b, 1999), which lead to consistent, but somewhat higher, deuterium abundances than those inferred from "standard" data reduction analyses.

Indeed, the absorption spectra of DI and HI are identical, except for a wavelength/velocity offset resulting from the heavier reduced mass of the deuterium atom. An HI "interloper", a low-column density cloud shifted by ~ 81 km s^-1 with respect to the main absorbing cloud, would masquerade as DI. If this is not accounted for, a D/H ratio which is too high would be inferred. Since there are more low-column density absorbers than those with high HI column densities, absorption-line systems with somewhat lower HI column density (e.g., Lyman-limit systems) are more susceptible to this contamination than are the higher HI column density absorbers (e.g., damped Ly absorbers). However, for the damped Ly absorbers, an accurate determination of the HI column density requires an accurate placement of the continuum, which could be compromised by interlopers. This might lead to an overestimate of the HI column density and a concomitant underestimate of D/H (J. Linsky, private communication). As will be seen, there is the possibility that each of these effects may have contaminated the current data. Indeed, complex velocity structure in the D'Odorico et al. (2001) absorber (see Levshakov et al. 2002) renders it of less value in constraining primordial deuterium, and it will not be included in the estimates presented here.

In Figure 4 are shown the extant data (circa June 2003) for D/H as a function of metallicity from the work of Burles & Tytler (1998a, b), O'Meara et al. (2001), Pettini & Bowen (2002), and Kirkman et al. (2003). Also shown for comparison are the local interstellar medium (ISM) D/H (Linsky & Wood 2000) and that for the presolar nebula as inferred from solar system data (Geiss & Gloeckler 1998).

Figure 4. The deuterium abundance, D/H, versus metallicity, "X" (usually, X = Si), from observations (as of early 2003) of QSOALS (filled circles). Also shown for comparison are the D abundances for the local ISM (filled square) and the solar system ("Sun"; filled triangle).

On the basis of our discussion of the post-BBN evolution of D/H, a "deuterium plateau" at low metallicity was expected. If, indeed, one is present, it is hidden by the dispersion in the current data. Given the possibility that interlopers may affect both the DI and the HI column density determinations, it is interesting to plot D/H as a function of N(HI). This is shown in Figure 5, where there is some (limited) evidence that D/H is higher in the Lyman-limit systems than in the damped Ly absorbers.

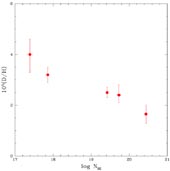Figure 5. The deuterium abundance, D/H, versus the HI column density in the absorbers, N(HI), for the same QSOALS as in Figure 4.

To decide how to utilize this confusing data it may be of value to consider the observations chronologically. Of the set chosen here, Burles & Tytler (1998a, b) studied the first two lines of sight. For PKS 1937-1009 they derived y_D 10⁵(D/H) = 3.25 ± 0.3 (Burles & Tytler 1998a), while for Q1009+299 they found y_D = 3.98^+0.59_-0.67 (Burles & Tytler 1998b). These two determinations are in excellent agreement with each other (² = 1.0), leading to a mean abundance <y_D> = 3.37 ± 0.27. Next, O'Meara et al. (2001) added the line of sight to HS 0105+1619, finding a considerably lower abundance y_D = 2.54 ± 0.23. Indeed, while the weighted mean for these three lines of sight is <y_D> = 2.88, the ² has ballooned to 6.4 (for two degrees of freedom). Absent any evidence that one or more of these abundances is in error, O'Meara et al. adopt the mean, and, for the error in the mean, they take the dispersion about the mean (0.72) divided by the square root of the number of data points: <y_D> = 2.88 ± 0.42. One year later Pettini & Bowen (2001) published their HST data on the line of sight toward Q2206-199, finding a surprisingly low value of y_D = 1.65 ± 0.35. Including this determination reduces the mean to <y_D> = 2.63, but the dispersion in y_D grows to 1.00 and ² = 16.3 for three degrees of freedom. Clearly, either one or more of these determinations is in error, or the variation among the high-redshift, low-metallicity deuterium abundances is larger than anticipated from our understanding of its evolution (Jedamzik & Fuller 1997). Using the mean and its dispersion (to fix the error), as of the time of the Carnegie Symposium, the best estimate for the primordial D abundance was <y_D> = 2.63 ± 0.50. Shortly thereafter, in early 2003, the data of Kirkman et al. (2003) appeared for the line of sight toward Q1243+3047. For this line of sight they find y_D = 2.42^+0.35_-0.25. This abundance lies between the lowest and the higher previous values, reducing the overall dispersion to 0.88, while hardly changing the mean from y_D = 2.63 to 2.60. While the total ² is still enormous, increasing slightly to 16.6, the reduced ² decreases from 5.4 to 4.2. This is still far too large, suggesting that one or more of these determinations may be contaminated, or that there may actually be real variations in D/H at high redshifts and low metallicities. Notice (see Fig. 5) that the largest D/H estimates are from the two absorbers with the lowest HI column densities (Lyman-limit systems), where interlopers might contribute to the inferred DI column densities, while the lowest abundances are from the higher HI column density (damped Ly ) absorbers, where interlopers might affect the wings of the HI lines used to fix the HI column densities. Absent any further data supporting, or refuting, these possibilities, there is no a priori reason to reject any of these determinations.

To utilize the current data, the weighted mean D abundances for these five lines of sight and the dispersion are used to infer the abundance of primordial deuterium (and its uncertainty) adopted in this review: y_D = 2.6 ± 0.4. Note that, given the large dispersion, two-decimal place accuracy seems to be wishful thinking at present. For this reason, in quoting the primordial D abundance inferred from the observational data I have purposely chosen to quote values to only one decimal place. This choice is consistent too with the ~ 3% - 8% theoretical uncertainty (at fixed ) in the BBN-predicted abundance. In Figure 6 are shown the data, along with the corresponding 1 band. It is worth remarking that using the same data Kirkman et al. (2003) derive a slightly higher mean D abundance: y_D = 2.74. The reason for the difference is that they first find the mean of log(y_D) and then use it to compute the mean D abundance (y_D 10^<log(y_D)>).

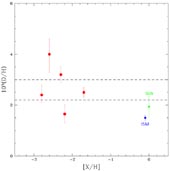Figure 6. As in Figure 4. The dashed lines represent the ± 1 band calculated from the mean and its dispersion ((D/H)P = 2.6 ± 0.4 × 10-5; see the text).