


4.4. The Baryon Density At 10 Gyr
Although the majority of baryons in the recent/present
universe are dark, it is still possible to constrain
the baryon density indirectly using observational data (see, e.g.
Steigman, Hata &
Felten 1999,
Steigman, Walker &
Zentner 2000;
Steigman 2001).
The magnitude-redshift relation determined by observations of type Ia
supernovae (SNIa) constrain the relation between the present matter
density ( M)
and that in a cosmological constant
(
M)
and that in a cosmological constant
(
 ).
The allowed region in the
).
The allowed region in the

 -
-  M plane
derived from the observations of
Perlmutter et
al. (1997),
Schmidt et al. (1998),
and Perlmutter et
al. (1999)
are shown in Figure 11.
M plane
derived from the observations of
Perlmutter et
al. (1997),
Schmidt et al. (1998),
and Perlmutter et
al. (1999)
are shown in Figure 11.
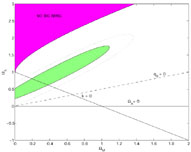 |
Figure 11. The 68% (solid) and 95% (dotted)
contours in the
|
If, in addition, it is assumed that the universe
is flat ( = 0; an assumption
supported by the CMB data), a reasonably accurate determination of
= 0; an assumption
supported by the CMB data), a reasonably accurate determination of
 M
results:
M
results:
 M(SNIa;
Flat) = 0.28+0.08-0.07
(Steigman, Walker &
Zentner 2000;
Steigman 2001).
But, how to go from the matter
density to the baryon density? For this we utilize rich
clusters of galaxies, the largest collapsed objects,
which provide an ideal probe of the baryon fraction
in the present universe fB. X-ray observations
of the hot gas in clusters, when corrected for the baryons
in stars (albeit not for any dark cluster baryons), can
be used to estimate fB. Using the
Grego et al. (2001)
observations of the Sunyaev-Zeldovich effect in clusters,
Steigman, Kneller &
Zentner (2002)
estimate fB and derive a present-universe
(t0
M(SNIa;
Flat) = 0.28+0.08-0.07
(Steigman, Walker &
Zentner 2000;
Steigman 2001).
But, how to go from the matter
density to the baryon density? For this we utilize rich
clusters of galaxies, the largest collapsed objects,
which provide an ideal probe of the baryon fraction
in the present universe fB. X-ray observations
of the hot gas in clusters, when corrected for the baryons
in stars (albeit not for any dark cluster baryons), can
be used to estimate fB. Using the
Grego et al. (2001)
observations of the Sunyaev-Zeldovich effect in clusters,
Steigman, Kneller &
Zentner (2002)
estimate fB and derive a present-universe
(t0  10 Gyr; z
10 Gyr; z  1)
baryon density:
1)
baryon density:
 10 =
5.1+1.8-1.4
(
10 =
5.1+1.8-1.4
( B
h2 = 0.019+0.007-0.005).
B
h2 = 0.019+0.007-0.005).