2.8. Gamma-ray bursts

2.8.1. Basic phenomenology

Gamma ray bursts (GRBs) are flashes of high energy radiation that can be brighter, during their brief existence, than any other gamma ray source in the sky. The bursts present an amazing variety of temporal profiles, spectra, and timescales that have puzzled astrophysicists for almost three decades [344]. In recent years, our observational insight of this phenomenon has been dramatically improved by the huge amount of data collected by the Burst and Transient Source Experiment (BATSE): several thousands GRB observations were obtained. New breakthrough results are the expected outcome of HETE-2 and Swift.

The temporal distribution of the bursts is one of the most striking signatures of the GRB phenomenon. There are at least four classes of distributions, from single-peaked bursts, including the fast rise and exponential decaying (FREDs) and their inverse (anti-FREDs), to chaotic structures (e.g. [345, 346]). Burst timescales go through the 30 ms scale to hundreds of seconds.

The GRB photon spectrum is well fitted in the BATSE detectors range, 20 keV to 2 MeV [344], by a combination of two power-laws, dn / d ^{( - 1)} ( is the flux density spectral index, F ⁺) with different values of at low and high energy [347]. Here, dn / d is the number of photons per unit photon energy. The break energy (where changes) in the observer frame is typically _b ~ 1 MeV, with 0 at energies below the break and -1 above the break. In several cases, the spectrum has been observed to extend to energies > 100 MeV [344, 348].

The angular distribution of these bursts is isotropic, and the paucity of comparatively faint bursts implies that we are seeing to near the edge of the source population [349]. Both effects, isotropy and non-homogeneity in the distribution, strongly suggest a cosmological origin of the phenomenon, confirmed by the detection of afterglows, delayed low energy emission of GRBs that allowed the measurement of the distance to the burst via a redshift determination of several GRB host-galaxies (e.g. [350, 351]).

2.8.2. The fireball model

The most popular interpretation of the GRB-phenomenology is that the observable effects are due to the dissipation of the kinetic energy of a relativistic expanding plasma wind, a "fireball", whose primal cause is not yet known [352, 353, 354, 355, 356, 357, 358] (see [359] for a detailed review). The rapid rise time and short duration, ~ 1 ms of the burst imply that the sources are compact, with a linear scale comparable to a light-ms, r₀ ~ 10⁷ cm. If the sources are so distant, the energy necessary to produce the observed events by an intrinsic mechanism is astonishing: about 10⁵² erg of rays must be released in less than 1 second. Compactness and high -ray luminosity implied by cosmological distances result in a very high optical depth to pair creation, since the energy of observed -ray photons is above the threshold for pair production. The number density of photons at the source n is

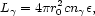(58)

where 1 MeV is the characteristic photon energy. Using r₀ ~ 10⁷cm, the optical depth for pair production at the source is

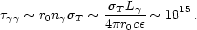(59)

The high optical depth creates the fireball: a thermal plasma of photons, electrons, and positrons. The radiation pressure on the optically thick source drives relativistic expansion, converting internal energy into the kinetic energy of the inflating shell [353, 354]. As the source expands, the optical depth is reduced. If the source expands with a Lorentz factor , the energy of photons in the source frame is smaller by a factor compared to that in the observer frame, and most photons may therefore be below the pair production threshold.

Baryonic pollution in this expanding flow can trap the radiation until most of the initial energy has gone into bulk motion with Lorentz factors of 10² - 10³ [360, 359]. The kinetic energy, however, can be partially converted into heat when the shell collides with the interstellar medium or when shocks within the expanding source collide with one another. The randomized energy can then be radiated by synchrotron radiation and inverse Compton scattering yielding non-thermal bursts with timescales of seconds, at large radius r = r_d > 10¹² cm, beyond the Thompson sphere. Relativistic random motions are likely to give rise to a turbulent build up of magnetic fields, and therefore to Fermi acceleration of charged particles.

Coburn and Boggs [361] recently reported the detection of polarization - a particular orientation of the electric-field vector - in the -rays observed from a burst. The radiation released through synchrotron emission is highly polarized, unlike in other previously suggested mechanisms such as thermal emission or energy loss by relativistic electrons in intense radiation fields. Thus, polarization in the -rays from a burst provides direct evidence in support of synchrotron emission as the mechanism of -ray production (see also [362]).

2.8.3. Fermi acceleration in dissipative wind models of GRBs

Following the Hillas' criterion, the Larmor radius r_L should be smaller than the largest scale l_GRB over which the magnetic field fluctuates, since otherwise Fermi acceleration will not be efficient. One may estimate l_GRB as follows. The comoving time, i.e., the time measured in the fireball rest frame, is t = r / c. Hence, the plasma wind properties fluctuate over comoving scale length up to l_GRB ~ r / , because regions separated by a comoving distance larger than r/ are causally disconnected. Moreover, the internal energy is decreasing because of the expansion and thus it is available for proton acceleration (as well as for -ray production) only over a comoving time t. The typical acceleration time scale is then [233]

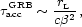(60)

where c is the Alfvén velocity. In the GRB scenario ~ 1, so Eq. (60) sets a lower limit on the required comoving magnetic field strength, and the Larmor radius r_L = E' / eB = E / eB, where E' = E / is the proton energy measured in the fireball frame.

This condition sets a lower limit for the required comoving magnetic field strength [233],

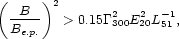(61)

where E = 10²⁰ E₂₀ eV, = 300₃₀₀, L = 10⁵¹L₅₁ erg s^-1 is the wind luminosity, and B_e.p. is the equipartition field, i.e. a field with comoving energy density similar to that associated with the random energy of the baryons.

The dominant energy loss process in this case is synchrotron cooling. Therefore, the condition that the synchrotron loss time of Eq. (31) be smaller than the acceleration time sets the upper limit on the magnetic field strength

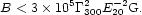(62)

Since the equipartition field is inversely proportional to the radius r, this condition may be satisfied simultaneously with (61) provided that the dissipation radius is large enough, i.e.

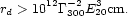(63)

The high energy protons lose energy also in interaction with the wind photons (mainly through pion production). It can be shown, however, that this energy loss is less important than the synchrotron energy loss [233].

A dissipative ultra-relativistic wind, with luminosity and variability time implied by GRB observations, satisfies the constraints necessary to accelerate protons to energy > 10²⁰ eV, provided that > 100, and the magnetic field is close to equipartition with electrons. We stress that the latter must be satisfied to account for both -ray emission and afterglow observations [360]. At this stage, it is worthwhile to point out that for the acceleration process at shocks with large the particle distributions are extremely anisotropic in shock, with the particle angular distribution opening angles ~ ^-1 in the upstream plasma rest frame. Therefore, when transmitted downstream the shock particles have a limitted chance to be scattered efficiently to re-eneter the shock [363]. However, in this particular case, the energy gain by any "successful" CR can be comparable to its original energy, i.e., < E> / E ~ 1.

2.8.4. UHECRs and GRBs: connections

In the GRB model for UHECR production described above ⁽³²⁾, the high energy CRs are protons accelerated by Fermi's mechanism in sources that are distributed throughout the universe [233, 366]. It is therefore possible to compare the UHECR spectrum with the prediction from a homogeneous cosmological distribution of sources, each generating a power law differential spectrum of high energy protons as typically expected from Fermi acceleration. Under the assumption that the GRB rate evolution is similar to the star-formation rate evolution, the local GRB rate is ~ 0.5 Gpc^-3 yr^-1 [367], implying a local -ray energy generation rate of 10⁴⁴ erg Mpc^-3 yr^-1. ⁽³³⁾

The energy observed in -rays reflects the fireball energy in accelerated electrons. If accelerated electrons and protons (as indicated by afterglow observations [368]) carry similar energy, then the GRB production rate of high energy protons is

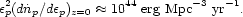(64)

The generation rate (Eq. 6) of high energy protons is remarkably similar to that required to account for the flux of > 10¹⁹ eV CRs, whereas in this model, the suppression of model flux above 10^19.7 eV is due to the GZK cutoff. Stecker and Scully and Stecker [369, 370] have raised doubts on the possibility of this generating a very strong cutoff at the highest CR energies, since if the GRB redshift distribution follows that of the star formation rate in the universe, a rate which is higher at larger redshift, most of the GRBs would be just too far and CR with energies above 3 × 10¹⁹ eV would be strongly attenuated by the CMB. For a HiRes-shape spectrum, a common origin between GRBs and ultrahigh energy CRs [371] is favored. ⁽³⁴⁾ For appraisals of this and other general criticisms made to the GRB-UHECR connection see [372, 373].

Two of the highest energy CRs come from directions that are within the error boxes of two remarkable GRBs detected by BATSE with a delay of (10) months after the bursts [374]. However, a rigorous analysis shows no correlation between the arrival direction of ultrahigh energy CRs and GRBs from the third BATSE catalog [375]. No correlations were found either between a pre-CGRO burst catalog and the Haverah Park shower set that covered approximately the same period of time. These analysis, however, could have been distorted by the angular resolution ( ~ 3°) of the GRB measurements. A sensitive anisotropy analysis between ultrahigh energy CRs and GRBs will be possible in the near future, using PAO, HETE-2 and Swift. Preliminary results (if one assumes that GRBs are most likely to happen in infrared luminous galaxies) do not seem to indicate any strong correlation (see above Section 2.7).

2.8.5. A GRB origin for CRs below the ankle?

Wick, Dermer and Atoyan [376] have recently proposed a model for the origin of all CRs above ~ 10¹⁴ eV / nucleon. In this model, GRBs are assumed to inject CR protons and ions into the interstellar medium of star-forming galaxies -including ours- with a power-law spectrum extending to a maximum energy ~ 10²⁰ eV. In addition to the more energetic, extragalactic spectrum of CR, the CR spectrum near the knee was also shown to be plausibly fitted with CRs trapped in the Galactic halo that were accelerated and injected by an earlier Galactic GRB. For power-law CR proton injection spectra with injection number index p 2 and low and high-energy cutoffs, normalization to the local time- and space-averaged GRB luminosity density implies that if this model is correct, the nonthermal content in GRB blast waves is hadronically dominated by a factor 60-200, limited in its upper value by energetic and spectral considerations. Neutrinos to be detected in kilometer-scale neutrino detectors such as IceCube (See Sec. 4) provide a clean signal of this model [377].

GRBs have been also proposed as possible progenitors of the CR anisotropy observed in the direction of the GC [378]. Specifically, because of adiabatic losses, the highest energy particles that emerge from GRBs are mostly neutrons (protons are captive in the magnetic field and suffer extensive adiabatic losses on the way out [379]) expected to be the carriers of directional signals. The predicted flux on Earth from the last GRB in the Galaxy ocurring, say 10⁶ yr ago, is ~ 10³¹ ers / s. This is just above the CR excess reported by AGASA [49] and SUGAR [52] collaborations.

³² Recently, an alternative scenario for UHECR production in GRBs originated in the collapse of a massive star into a black hole endowed with electromagnetic structure has been suggested [364] (see also [365]). Back.

³³ The local (z = 0) energy production rate in -rays by GRBs is roughly given by the product of the characteristic GRB -ray energy, E 2 × 10⁵³ erg, and the local GRB rate. Back.

³⁴ In addition, dispersion of magnetic fields in the intergalactic medium can make the number of UHECR-contributing GRBs to grow above the burst rate within the GZK sphere. The latter, within 100 Mpc from Earth, is in the range of 10^-2 to 10^-3 yr^-1. Assuming a dispersion tiemscale, t ~ 10⁷ yr, the number of sources contributing to the flux at any given time may be as large as ~ 10⁴ [233]. Back.