


4.2. Astronomy on Ice
IceCube is, perhaps, the most promising route for neutrino detection
[495].
This telescope will consist of 80
kilometer-length strings, each instrumented with 60 10-inch
photomultipliers spaced by 1.7 m. The deepest module is 2.4 km
below the ice surface. The strings are arranged at the apexes of
equilateral triangles 125 m on a side. The instrumented detector
volume is a cubic kilometer.
(43) A surface air
shower detector, IceTop, consisting of 160 Auger-style
Cerenkov detectors deployed over 1 km2 above IceCube,
augments the deep-ice component by providing a tool for
calibration, background rejection and air-shower physics. Muons
can be observed from 1011 eV to 1018 eV. Cascades,
generated by  e,
e,
 e,
e,

 , and
, and

 can be observed above
1011 eV and reconstructed at
energies somewhat above 1013 eV. The angular resolution is
can be observed above
1011 eV and reconstructed at
energies somewhat above 1013 eV. The angular resolution is
 0.7° at TeV
energies.
0.7° at TeV
energies.
As an example of the IceCube potential, in what follows we briefly
discuss its sensitivity to probe the neutron hypothesis of UHECRs
via observation of the antineutrino beam
n  p +
e- +
p +
e- +
 e, expected
from the Cygnus direction
[54].
To this end, we first estimate the background signal. As discussed in
Sec. 2.1, the TeV
e, expected
from the Cygnus direction
[54].
To this end, we first estimate the background signal. As discussed in
Sec. 2.1, the TeV
 -ray flux,
-ray flux,
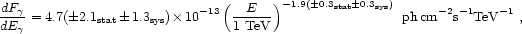 |
(75) |
reported by HEGRA Collaboration
[139]
in the vicinity of Cygnus OB2 is likely due to hadronic processes. Since
 0's,
0's,
 +'s, and
+'s, and
 -'s are produced in
equal numbers, we expect two photons, two
-'s are produced in
equal numbers, we expect two photons, two
 e's, and four
e's, and four
 µ's per
µ's per
 0. On average, the
photons carry one-half of the energy of the pion, and the neutrinos
carry one-quarter. For
dF
0. On average, the
photons carry one-half of the energy of the pion, and the neutrinos
carry one-quarter. For
dF /
dE
/
dE
 E
E -2,
the energy-bins dE scale with these fractions, and we arrive at
-2,
the energy-bins dE scale with these fractions, and we arrive at
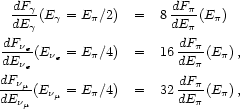 |
(76) |
for the fluxes at the source, where
 denotes any one of the
three pion charge-states. Terrestrial experiments (see e.g.
[504])
have shown that
denotes any one of the
three pion charge-states. Terrestrial experiments (see e.g.
[504])
have shown that
 µ and
µ and

 are maximally mixed with a mass-squared difference
~ 10-3 eV2. This implies that the
are maximally mixed with a mass-squared difference
~ 10-3 eV2. This implies that the
 µ's will partition
themselves equally between
µ's will partition
themselves equally between
 µ's and
µ's and

 's on lengths
large compared to the oscillation length
's on lengths
large compared to the oscillation length
 osc ~ 1.5
× 10-3
(E
osc ~ 1.5
× 10-3
(E / PeV)
pc. From these remarks, one finds a nearly identical flux for each of
the three neutrino flavors (j = e, µ,
/ PeV)
pc. From these remarks, one finds a nearly identical flux for each of
the three neutrino flavors (j = e, µ,
 ), which is equal to
[155]
), which is equal to
[155]
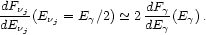 |
(77) |
Although TeV neutrinos are copiously produced, because they are
weakly interacting the detection probability on Earth is tiny,
about 10-6
[466].
In particular, the expected
 event rate at
IceCube associated with the
unidentified HEGRA source is < 1 yr-1 (D. Hooper, private
communication). Such an event rate is even smaller than the
atmospheric neutrino background.
(44)
Moreover, existing limits on TeV
event rate at
IceCube associated with the
unidentified HEGRA source is < 1 yr-1 (D. Hooper, private
communication). Such an event rate is even smaller than the
atmospheric neutrino background.
(44)
Moreover, existing limits on TeV
 -ray fluxes in
this region of the sky are near the HEGRA sensitivity
[505].
In light of this, we take as background the atmospheric neutrino event
rate, and so Poisson statistics implies that a signal
-ray fluxes in
this region of the sky are near the HEGRA sensitivity
[505].
In light of this, we take as background the atmospheric neutrino event
rate, and so Poisson statistics implies that a signal
 3.5 events is significant
at the 95% CL.
3.5 events is significant
at the 95% CL.
Antineutrinos take only a very small part of the energy of the parent neutron, typically ~ 10-3. Hence, to estimate the event rate of TeV antineutrinos at IceCube, the relevant nucleus population at the source has an energy per nucleon EN, PeV ~ 1 PeV. Nuclei with Lorentz factor ~ 106 are synthesized in all supernovae. Hadronic interactions with the HII population (density < 30 cm-3 [140]) and photodisintegration processes provide the flux of PeV neutrons. In this energy regime, the target photons at photodisintegration threshold energies are in the ultraviolet, ~ 5 eV. This includes the entire emission spectrum of the O stars and about 60% of photons from B stars (with average temperature 28,000 K). From the photon emission rate FUV the number density nUV at the surface of a sphere of radius R from the core center is given by
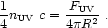 |
(78) |
For the O-star population, the photon emission rate in the Lyman
region is found to be FL
 1051 photons
s-1
[192].
The Lyman emission corresponds
to 60% of the entire O star spectrum. Furthermore, as mentioned
above, 60% of the B star spectrum is also active for
photodisintegration in this energy region, and the B star
population is about 20 times greater than that of the O stars
[192].
Now, from the H-R diagram
[506]
one can infer that the energy luminosity of a B-star is about 0.1 that
of an O star.
Additionally, the B star temperature is about 0.5 the O star
temperature, giving a number luminosity ratio of about 0.2. All in
all, for photodisintegration resulting in PeV nucleons, the
relevant photon density in the core of the Cygnus OB2 association
is nUV ~ 230 cm-3. The nucleus mean free
path is
1051 photons
s-1
[192].
The Lyman emission corresponds
to 60% of the entire O star spectrum. Furthermore, as mentioned
above, 60% of the B star spectrum is also active for
photodisintegration in this energy region, and the B star
population is about 20 times greater than that of the O stars
[192].
Now, from the H-R diagram
[506]
one can infer that the energy luminosity of a B-star is about 0.1 that
of an O star.
Additionally, the B star temperature is about 0.5 the O star
temperature, giving a number luminosity ratio of about 0.2. All in
all, for photodisintegration resulting in PeV nucleons, the
relevant photon density in the core of the Cygnus OB2 association
is nUV ~ 230 cm-3. The nucleus mean free
path is  35 kpc,
corresponding to a collision time
35 kpc,
corresponding to a collision time
 = 105
yr. Thus, the collision rate for photodisintegration in the core
region is comparable to the hadronic interaction
rate. (45)
= 105
yr. Thus, the collision rate for photodisintegration in the core
region is comparable to the hadronic interaction
rate. (45)
Since one is interested in neutrinos, it is still
necessary to compare the production rate for charged pions in the
hadronic case to the overall rate for generating neutrons. To
assess this ratio, we made use of available high energy event
simulations showing spectator nucleon and pion spectra
for Fe-N / p-N collisions at 1015 and 1016 eV
[507]
(summarized in
[508]).
The pion rapidity spectra in the central
plateau are roughly energy independent, except for the widening
of the plateau with energy whereas
there is a slow increase of spectator neutrons as one reaches the
region of interest (EN
 1 PeV). Allowing for sizeable differences
in hadronic interaction models, the secondary populations are roughly
35%
1 PeV). Allowing for sizeable differences
in hadronic interaction models, the secondary populations are roughly
35%  ±, 45%
±, 45%
 , 10%
nucleons, and 10% K
[508].
In the energy range yielding PeV neutrons, only about 30% of the rapidity
plateau contributes charged pions above 2 TeV. Since only half the
nucleons are neutrons, we arrive at a ratio
, 10%
nucleons, and 10% K
[508].
In the energy range yielding PeV neutrons, only about 30% of the rapidity
plateau contributes charged pions above 2 TeV. Since only half the
nucleons are neutrons, we arrive at a ratio
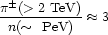 |
(79) |
in the hadronic interactions.
However, photodisintegration also takes place in the outer regions of the
OB association as long as: (i) the density of the optical photons
propagating out from the core allows a reaction time
which is smaller than the age of the cluster ~ 2.5 Myr
[509]
and (ii) the diffusion front of the nuclei has passed the region in
question. From Eq. (78) we estimate
an average photon density nUV
 25
cm-3 out to 30 pc, which gives a reaction time of
25
cm-3 out to 30 pc, which gives a reaction time of
 106
yr. The diffusion time
(~ 1.2 Myr) is a bit smaller than the age of the cluster,
and somewhat higher than the reaction time, allowing about 90% of the
nuclei to interact
during the lifetime of the source. Thus, the production rate of neutrons
via photodisintegration is amplified by a volume factor of 27 over the rate
in the 10 pc core. The net result of all this consideration is that the
PeV neutron population is about an order of magnitude greater than that
of the TeV charged pions
[54].
106
yr. The diffusion time
(~ 1.2 Myr) is a bit smaller than the age of the cluster,
and somewhat higher than the reaction time, allowing about 90% of the
nuclei to interact
during the lifetime of the source. Thus, the production rate of neutrons
via photodisintegration is amplified by a volume factor of 27 over the rate
in the 10 pc core. The net result of all this consideration is that the
PeV neutron population is about an order of magnitude greater than that
of the TeV charged pions
[54].
With this in mind, we now discuss the prospects for a new multi-particle
astronomy: neutrons as directional pointers + antineutrinos as inheritors
of directionality. The basic formula that relates the neutron flux at the
source (dFn / dEn) to the
antineutrino flux observed at Earth
(dF / dE
/ dE ) is
[54]:
) is
[54]:
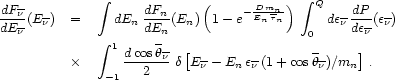 |
(80) |
The variables appearing in Eq. (80) are the antineutrino and
neutron energies in the lab
(E and En),
the antineutrino angle with respect to the direction of the
neutron momentum, in the neutron rest-frame
(
and En),
the antineutrino angle with respect to the direction of the
neutron momentum, in the neutron rest-frame
(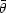
 ),
and the antineutrino energy in the neutron rest-frame
(
),
and the antineutrino energy in the neutron rest-frame
(
 ).
The last three variables are not observed
by a laboratory neutrino-detector, and so are integrated over.
The observable
E
).
The last three variables are not observed
by a laboratory neutrino-detector, and so are integrated over.
The observable
E is
held fixed. The delta-function relates the neutrino energy in the lab to
the three integration variables.
(46)
The parameters appearing in Eq. (80) are the
neutron mass and rest-frame lifetime (mn and
is
held fixed. The delta-function relates the neutrino energy in the lab to
the three integration variables.
(46)
The parameters appearing in Eq. (80) are the
neutron mass and rest-frame lifetime (mn and
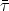 n),
and the distance to the neutron source (D).
dFn / dEn is the neutron flux at the
source, or equivalently, the neutron flux that would be observed
from the Cygnus region in the absence of neutron decay. Finally,
dP / d
n),
and the distance to the neutron source (D).
dFn / dEn is the neutron flux at the
source, or equivalently, the neutron flux that would be observed
from the Cygnus region in the absence of neutron decay. Finally,
dP / d

 is the
normalized probability that the decaying neutron in its rest-frame
produces a
is the
normalized probability that the decaying neutron in its rest-frame
produces a  e
with energy
e
with energy

 .
Setting the beta-decay neutrino energy
.
Setting the beta-decay neutrino energy

 equal to its mean value
equal to its mean value

 0, we have
dP / d
0, we have
dP / d

 =
=
 (
(
 -
-
 0).
(47)
Here, the maximum neutrino energy in the
neutron rest frame is just the neutron-proton mass-difference
Q
0).
(47)
Here, the maximum neutrino energy in the
neutron rest frame is just the neutron-proton mass-difference
Q  mn - mp = 1.29 MeV,
and the minimum neutrino energy is zero in the massless limit.
(48)
The expression in parentheses in Eq. (80) is the decay
probability for a neutron with lab energy En,
traveling a distance D. In principle, one should consider a
source distribution, and integrate over the volume
mn - mp = 1.29 MeV,
and the minimum neutrino energy is zero in the massless limit.
(48)
The expression in parentheses in Eq. (80) is the decay
probability for a neutron with lab energy En,
traveling a distance D. In principle, one should consider a
source distribution, and integrate over the volume
 d3 D.
Instead, we will take D to be the 1.7 kpc distance from Earth to
Cygnus OB2; for the purpose of generating the associated neutrino flux,
this cannot be in error by too much.
d3 D.
Instead, we will take D to be the 1.7 kpc distance from Earth to
Cygnus OB2; for the purpose of generating the associated neutrino flux,
this cannot be in error by too much.
Putting all this together, normalization to the observed "neutron"
excess at
~ 1018 eV leads to about 20 antineutrino events at IceCube per
year [54].
A direct TeV
 e event in
IceCube will make a showering event, which, even if seen, provides
little angular resolution. In the energy region below 1 PeV,
IceCube will resolve directionality only for
e event in
IceCube will make a showering event, which, even if seen, provides
little angular resolution. In the energy region below 1 PeV,
IceCube will resolve directionality only for
 µ and
µ and
 µ.
Fortunately, neutrino oscillations rescue the signal.
Since the distance to the Cygnus region greatly exceeds the
µ.
Fortunately, neutrino oscillations rescue the signal.
Since the distance to the Cygnus region greatly exceeds the
 e
oscillation length
e
oscillation length
 osc ~
10-2(E
osc ~
10-2(E / PeV) pc (taking the solar
oscillation scale
/ PeV) pc (taking the solar
oscillation scale
 m2 ~
10-5 eV2), the
antineutrinos decohere in transit. The arriving antineutrinos are
distributed over flavors, with the muon antineutrino flux
F
m2 ~
10-5 eV2), the
antineutrinos decohere in transit. The arriving antineutrinos are
distributed over flavors, with the muon antineutrino flux
F µ given by the factor
1/4 sin2(2
µ given by the factor
1/4 sin2(2 
 )
)
 0.20 times the original
F
0.20 times the original
F e flux. The
e flux. The

 flux is the same, and the
flux is the same, and the
 e
flux is 0.6 times the original flux. Here we have utilized for the
solar mixing angle the most recent SNO result
e
flux is 0.6 times the original flux. Here we have utilized for the
solar mixing angle the most recent SNO result


 32.5°
[510],
along with maximal mixing for
atmospheric
32.5°
[510],
along with maximal mixing for
atmospheric  µ-
µ-
 neutrinos and a negligible
neutrinos and a negligible
 e component in the
third neutrino eigenstate. All in all,
for a year of running at IceCube, one expects 4
e component in the
third neutrino eigenstate. All in all,
for a year of running at IceCube, one expects 4
 µ
showers with energies
µ
showers with energies
 1 TeV to cluster
within 1° of the source direction, comfortably above the
stated CL
[54].
1 TeV to cluster
within 1° of the source direction, comfortably above the
stated CL
[54].
IceCube is not sensitive to TeV neutrinos from the Galactic Center, as these are above the IceCube horizon, where atmospheric muons will dominate over any signal. However, other kilometer-scale neutrino detectors, such as those planned for the Mediterranean Sea, may see the Galactic Center flux.
In summary,
in a few years of observation, IceCube will attain
5 sensitivity for discovery of the Fe
sensitivity for discovery of the Fe
 n
n

 e
e

 µ
cosmic beam, providing the
"smoking ice" for the Galactic Plane neutron hypothesis.
µ
cosmic beam, providing the
"smoking ice" for the Galactic Plane neutron hypothesis.
43 Extension of these aperture is in the proposal stage [503]. Back.
44 For a year of running at
IceCube the expected background from atmospheric neutrinos (with
energy  1 TeV) within
1° circle centered in the
Cygnus direction (about 40° below the horizon) is < 1.5 events.
Back.
1 TeV) within
1° circle centered in the
Cygnus direction (about 40° below the horizon) is < 1.5 events.
Back.
45 This estimate takes into account a
hadronic cross section,
 Fe p ~
A0.75
Fe p ~
A0.75
 pp
pp
 6 ×
10-25 cm2, and the generous upper limit
[138]
of the nucleon density ~ 30 cm-3
[140].
Back.
6 ×
10-25 cm2, and the generous upper limit
[138]
of the nucleon density ~ 30 cm-3
[140].
Back.
46 Note that
E =
=
 n(
n(
 +
+


 cos
cos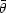
 = En
= En

 (1 +
cos
(1 +
cos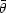
 / mn,
/ mn,
where
 n =
En / mn is the Lorentz factor, and
(as usual)
n =
En / mn is the Lorentz factor, and
(as usual)

 1 is the particle's
velocity in units of c.
Back.
1 is the particle's
velocity in units of c.
Back.
47 The
delta-function in the neutron frame gives rise to a flat
spectrum for the neutrino energy in the lab for fixed neutron
lab-energy En =
 n
mn:
n
mn:
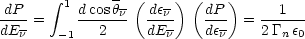 |
with 0  E
E
 2
2
 n
n
 0.
Back.
0.
Back.
48 The
massless-neutrino approximation seems justifiable here:
even an eV-mass neutrino produced at rest in the neutron
rest-frame would have a lab energy of
m
 n
n
 GeV,
below threshold for neutrino telescopes.
Back.
GeV,
below threshold for neutrino telescopes.
Back.