5.2. Formation

The rate at which stars with number density n encounter target stars with number density n_c in a cluster with dispersion velocity v is given by (e.g. Hut & Verbunt 1983):

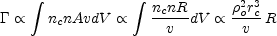(5)

where A is the interaction cross section (proportional to R / v² because of gravitational focusing), R the radius of the star, _o is the central mass density and r_c the core radius. Because the number densities of stars drop rapidly with distance from the cluster center, the integral over volume dV can be approximated by multiplying the central encounter rate with the volume of the cluster core. An analogous equation gives the exchange encounter rate

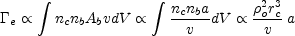(6)

where n_b is the number of binaries per unit volume, and a the semi-major axis of the binary. The ratio of tidal capture to exchange encounters is roughly

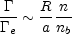(7)

The velocity dispersion v is related to the core mass and radius through (a specific version of) the virial theorem (King 1966):

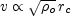(8)

Therefore (Verbunt 2003)

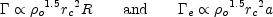(9)

Because neutron stars are formed with appreciable velocities, a cluster with a high mass is expected to retain a higher fraction of the neutron stars that are formed in it than a cluster with a low mass. In a cluster with strong mass segregation, virtually all the neutron stars will have migrated to the core. Thus a massive cluster with strong mass segregation is expected to have a much higher central number density of neutron stars than a low-mass little-segregated cluster. Thus, the ratio n_c / _o for neutron stars, and through this the proportionality constant for the last members of Eqs. 5 and 6 will vary widely between clusters (Verbunt & Meylan 1988). On the other hand, white dwarfs are always retained upon formation, and due to their lower masses are less affected by mass segregation. This is probably the reason that the relation between the number of X-ray sources (mainly cataclysmic variables) and is as narrow as shown in Figure 13.

Due to the large number density of stars in a cluster core, an appreciable fraction of neutron stars in that core may be involved in a close encounter with a single star or with a binary. The formation of tidal bulges in a passage of a neutron star within ~ 3 times the radius of a main-sequence star drains enough energy from the relative orbit of the two stars to bind them in a binary. This process is called tidal capture (Fabian et al. 1975). Whether it is efficient in the formation of a binary with a neutron star is under debate, because of the large amount of energy residing in the initially very eccentric orbit of the newly formed binary. If the orbit circularizes rapidly because of tides on the main sequence star, the energy released is enough to (almost) destroy the main sequence star (Ray et al. 1987, Verbunt 1994). Rapid circularization can be avoided if the energy exchange between tides and orbit is chaotic, as is likely in a highly eccentric orbit (Mardling 1995). Mass loss from the main-sequence star due to tidal heating may further limit the damage to the deeper layers of the star.

A neutron star can also be exchanged into a pre-existing binary when it takes the place of one of the binary members in an exchange encounter (Hills 1976). Which of the two mechanisms is more important depends on the number of binaries present in the core and on their orbital period distribution; as well as on the efficiency of the tidal capture process.

If a binary is of a type that very rarely results from the evolution of a primordial binary, then its presence in a globular cluster may be ascribed to formation via a close encounter. Such is the case for binaries with a neutron star. If a binary is very frequently formed from a primordial binary, then it is likely to be primordial also when present in a globular cluster. This is the case for magnetically active close binaries. Cataclysmic variables are somewhere in between, and thus in clusters can be formed both via close encounters and via evolution of a primordial binary. Figure 13 shows that the number of binaries with L_x 4 × 10³⁰ erg s^-1 scales well with the number of encounters in a cluster. Since most binaries with such luminosities are cataclysmic variables this implies that most cataclysmic variables are in fact formed via close encounters. One reason for this is that evolution from a primordial binary into a cataclysmic variable passes through a stage in which the binary is very wide; such a wide binary is easily unbound in a globular cluster by a passing star and the formation of a cataclysmic variable is prevented (Davies 1997). If the number of cataclysmic variables increases more slowly with central density than as _o^1.5, as suggested by Heinke et al. (2003d), this could suggest that primordial binaries do still contribute to the formation of cataclysmic variables. Remarkably, Jordán et al. (2004) find that the probability for a globular cluster associated with NGC4486 (M87) to harbor a bright X-ray source also scales with a lower power of _o than the collision number, i.e. roughly as _o^-0.5.

Looking now at the period distribution of the cataclysmic variables and low-mass X-ray binaries in globular clusters, we see that their periods are short, 1d. This may indicate that they are formed at short periods, which hints at tidal capture as the main formation process. Some care is necessary before one jumps to conclusions, however. Mass transfer in wide binaries tends to be faster, and thus wide binaries live shorter, and will be less numerous even if their formation rate is the same as that of short binaries. Also, longer periods are more difficult to measure, and some of the many binaries with unknown periods may have long periods. In addition, a wide binary with a neutron star or white dwarf can become closer via encounters with field stars. We doubt that this process is sufficiently efficient, given the observed presence in 47Tuc of active binaries with periods up to ten days that apparently have avoided further shrinking of their orbits. On the whole we tend to conclude that rumors of the death of the tidal capture model for the formation of binaries with a neutron star and of cataclysmic variables have been much exaggerated.

That exchange encounters do occur in globular clusters is evident from the wide pulsar binaries, such as M4 PSRA (P_b = 191d, Thorsett et al. 1999) and M53 PSRA (255d, Kulkarni et al. 1991). These are found in clusters with a relatively low central density, which allows long period binaries to survive (e.g. Verbunt 2003). They must have evolved from binaries with initial periods too long to be formed by tidal capture, in which the neutron star can thus only have entered via an exchange encounter. (M15 PSRC is an eccentric binary of two neutron stars in the outskirts of M15, and is another product of an exchange encounter: Phinney & Sigurdsson 1991.)

Acknowledgements

We are very grateful for comments, suggestions and help from Lorella Angelini, Keith Ashman, Pauline Barmby, Cees Bassa, Boris Dirsch, Rosanne Di Stefano, Josh Grindlay, Bill Harris, Piet Hut, Andres Jordán, Arunav Kundu, Erik Kuulkers, Tom Maccarone, Dave Pooley, Katherine Rhode, Craig Sarazin, Rudy Wijnands, and Steve Zepf.