


Sérsic's (1963; 1968) R1/n model is most commonly expressed as an intensity profile, such that
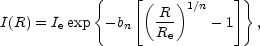
| (1) |
where Ie is the intensity at the effective radius Re that encloses half of the total light from the model (Caon et al. 1993; see also Ciotti 1991, his Equation 1). The constant bn is defined in terms of the third and final parameter n which describes the `shape' of the light-profile, and is given below. 2
One can integrate Equation (1) over a projected area
A =  R2 to obtain the luminosity, L, interior to any
radius R. This is
simply a matter of solving the integral
3
R2 to obtain the luminosity, L, interior to any
radius R. This is
simply a matter of solving the integral
3
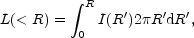
|
which yields, after substituting in x = bn(R / Re)1/n,

| (2) |
where  (2n,x)
is the incomplete gamma function defined by
(2n,x)
is the incomplete gamma function defined by
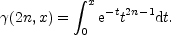
| (3) |
Replacing
 (2n,
x) with
(2n,
x) with
 (2n) in
Equation (2) gives one the value of Ltot
(Ciotti 1991).
(2n) in
Equation (2) gives one the value of Ltot
(Ciotti 1991).
Thus, the value of bn which we saw in Equation (1) is such that
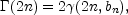
| (4) |
where  is the
(complete) gamma function
(Ciotti 1991).
Common values of bn are
b4 = 7.669 and
b1 = 1.678. In passing we note a useful property of the
is the
(complete) gamma function
(Ciotti 1991).
Common values of bn are
b4 = 7.669 and
b1 = 1.678. In passing we note a useful property of the
 function, which
is,
function, which
is,  (2n) =
(2n - 1)!.
(2n) =
(2n - 1)!.
Analytical expressions which approximate the
value of bn have been developed.
Capaccioli (1989)
provided one of the first such approximations such that
bn = 1.9992n - 0.3271, for
0.5 < n < 10 (see also
Prugniel & Simien
1997,
their equation A3a).
Ciotti & Bertin (1999)
showed
bn  2n - 1/3 for large values of n, and in practice this
provides a better fit for values of n greater than about 8
(see Graham 2001a,
his Figure 2).
Ciotti & Bertin (1999)
also provided an asymptotic expansion which, for values
of n > 0.36, is accurate to better than 10-4 and the
approximation of choice. For smaller values of n,
MacArthur, Courteau, &
Holtzman (2003)
provide a fourth order polynomial which
is accurate to better than two parts in 103 (see their Figure
23). However, the exact value of bn in Equatio (4) can
be solved numerically, and fast codes exist to do this,
2n - 1/3 for large values of n, and in practice this
provides a better fit for values of n greater than about 8
(see Graham 2001a,
his Figure 2).
Ciotti & Bertin (1999)
also provided an asymptotic expansion which, for values
of n > 0.36, is accurate to better than 10-4 and the
approximation of choice. For smaller values of n,
MacArthur, Courteau, &
Holtzman (2003)
provide a fourth order polynomial which
is accurate to better than two parts in 103 (see their Figure
23). However, the exact value of bn in Equatio (4) can
be solved numerically, and fast codes exist to do this,
For an exponential (n = 1) profile, 99.1% of the flux resides within the inner 4 Re (90.8% within the inner 4 scale-lengths) and 99.8% of the flux resides within the inner 5 Re (96.0% within the inner 5 scale-lengths). For an n = 4 profile, 84.7% of the flux resides with the inner 4 Re and 88.4% within the inner 5 Re.
Multiplying the negative logarithm of the luminosity profile (Equation 2) by 2.5 gives the enclosed magnitude profile, known as the "curve of growth",
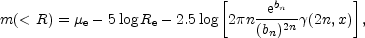
| (5) |
which asymptotes to the total apparent magnitude mtot
as R tends to infinity and, consequently,
 (2n,
x)
(2n,
x) 
 (2n)
(Figure 1).
(2n)
(Figure 1).
Multiplying the negative logarithm of Equation (1) by 2.5 yields the surface brightness profile (Figure 1), as used in Caon et al. (1993),
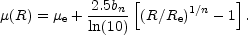
| (6) |
2.1.1. Asymptotic behavior for large n
For large values of n, the Sérsic model tends to a power-law with slope equal to 5. Substituting et = z = R / Re into Equation (1), one has
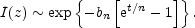
|
Now, for large n, et/n is small, and so one can use et/n ~ 1 + t / n. One can also use bn ~ 2n to give
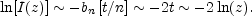
|
Thus µ(z) = - 2.5 log[I(z)] ~ 5 log(z).
For simplicity, the subscript `n' will be dropped from the term bn in what follows.
2 It is common for researchers studying dwarf galaxies to replace the exponent 1/n with n. In this case, de Vaucouleurs' model would have n = 0.25, rather than 4. Back.
3 Obviously if one is using a major- or minor-axis profile, rather than the geometric mean (R = (ab)1/2) profile, an ellipticity term will be required. This is trivial to add and for the sake of simplicity won't be included here. The issue of ellipticity gradients is more difficult, and interested readers should look at Ferrari et al. (2004). Back.