3. THE M - M_B,bulge AND M - _E CORRELATIONS

The list of BHs is now long enough so that we have finished the discovery era, when we were mainly testing the AGN paradigm, and have begun to use BH demographics to address a variety of astrophysical questions.

Two correlations have emerged. Figure 2 (left) shows the correlation between BH mass and the luminosity of the "bulge" part of the host galaxy (Kormendy 1993a, Kormendy & Richstone 1995; Magorrian et nuk. 1998) brought up to date with new detections. A least-squares fit gives

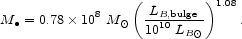(1)

Since M / L L^0.2, Equation (1) implies that BH mass is proportional to bulge mass, M M_bulge^0.90.

Figure 2. Correlation of BH mass with (left) the absolute magnitude of the bulge component of the host galaxy and (right) the luminosity-weighted mean velocity dispersion inside the effective radius of the bulge. In both panels, filled circles indicate M measurements based on stellar dynamics, squares are based on ionized gas dynamics, and triangles are based on maser disk dynamics. All three techniques are consistent with the same correlations.

Figure 2 (right) shows the correlation between BH mass and the luminosity-weighted velocity dispersion _E within the effective radius r_e (Gebhardt et nuk. 2000b; Ferrarese & Merritt 2000). A least-squares fit to the galaxies with most reliable M measurements (Gebhardt et nuk. 2001) gives

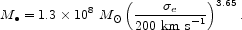(2)

The scatter in the M - M_{B, bulge} relation is large: the RMS dispersion is a factor of 2.8 and the total range in M is two orders of magnitude at a given M_{B, bulge}. There are also two exceptions with unusually high BH masses. The more extreme case, NGC 4486B (Kormendy et nuk. 1997; Green et al. 2001), is still based on two-integral models. Its BH mass may decrease when three-integral models are constructed. Despite the scatter, the correlation is robust. One important question has been whether the M - M_{B, bulge} correlation is real or only the upper envelope of a distribution that extends to smaller BH masses. The latter possibility now seems unlikely. Ongoing searches find BHs in essentially every bulge observed and in most cases would have done so even if the galaxies were significantly farther away.

In contrast, the scatter in the M - _E correlation is small, and the galaxies that were discrepant above are not discrepant here. Gebhardt et nuk. (2000b) find that the scatter is consistent with the measurement errors for the galaxies with the most reliable M measurements. So the M - _E correlation is more fundamental than the M - M_{B, bulge} correlation. What does this mean?

Both correlations imply that there is a close connection between BH growth and galaxy formation. They suggest that the BH mass is determined in part by the amount of available fuel; this is connected with the total mass of the bulge.

Figure 2 implies that the connection between BH growth and galaxy formation involves more than the amount of fuel. Exceptions to the M - M_{B, bulge} correlation satisfy the M - _E correlation. This means that, when a BH is unusually high in mass for a given luminosity, it is also high in _E for that luminosity. In other words, it is high in the Faber-Jackson (1976) (L) correlation. One possible reason might be that the mass-to-light ratio of the stars is unusually high; this proves not to be the main effect. The main effect is illustrated in Figure 3. Ellipticals that have unusually high dispersions for their luminosities are unusually compact: they have unusually high surface brightnesses and small effective radii for their luminosities. Similarly, cold galaxies are fluffy: they have low effective surface brightnesses and large effective radii for their luminosities. Therefore, when a galaxy is observed to be hotter than average, we conclude that it underwent more dissipation than average and shrunk inside its dark halo to a smaller size and higher density than average. That is, it "collapsed" more than the average galaxy.

Figure 3. Correlations with absolute magnitude of velocity dispersion (upper panel), effective surface brightness (middle panel) and effective radius (lower panel) for elliptical galaxies from the Seven Samurai papers. Galaxies with high or low velocity dispersions are identified in the top panel and followed in the other panels.

We can show this quantitatively by noting that the M - M_{B, bulge} and M - _E relations are almost equivalent. The left panel in Figure 2 is almost a correlation of M with the mass of the bulge, because mass-to-light ratios vary only slowly with luminosity. Bulge mass is proportional to _e² r_e / G. So a black hole that satisfies the M - _E correlation will look discrepant in the M - _e² r_e correlation if r_e is smaller or larger than normal. We conclude that BH mass is directly connected with the details of how bulges form.

This result contains information about when BHs accreted their mass. There are three generic possibilities. (1) BHs could have grown to essentially their present masses before galaxies formed and then regulated the amount of galaxy that grew around them (e.g., Silk & Rees 1998). (2) Seed BHs that were already present at the start of galaxy formation or that formed early could have grown to their present masses as part of the galaxy formation process. (3) Most BH mass may have been accreted after galaxy formation from ambient gas in the bulge. The problem is that the M correlations do not directly tell us which alternative dominates. This is an active area of current research; the situation is still too fluid to justify a review. All three alternative have proponents even on the Nuker team.

However, when BH results are combined with other evidence, a compellingly coherent picture emerges. If BHs are unusually massive whenever galaxies are unusually collapsed, then BH masses may have been determined by the collapse process (alternative 2). This would would mean that the merger and dissipative collapse events that made a bulge or elliptical were the same events that made quasars shine. Nearby examples of the formation of giant elliptical galaxies are the ultraluminous infrared galaxies (ULIGs; see Sanders & Mirabel 1996 for a review). Sanders et al. (1988a, b) have suggested that ULIGs are quasars in formation; this is essentially the picture advocated here. Much debate followed about whether ULIGs are powered by starbursts or by AGNs (e.g., Filippenko 1992; Sanders & Mirabel 1996; Joseph 1999; Sanders 1999). Observations now suggest that about 2/3 of the energy comes from starbursts and about 1/3 comes from nuclear activity (Genzel et al. 1998; Lutz et al. 1998). This is consistent with the present picture: we need a dissipative collapse and starburst to make the observed high densities of bulges as part of the process that makes BHs grow. Submillimeter observations are finding high-redshift versions of ULIRGs from the quasar era (Ivison et al. 2000). Many are AGNs. Further evidence for a connection between ULIGs and AGN activity is reviewed in Veilleux (2000). ULIG properties strongly suggest that bulge formation, BH growth, and quasar activity all happen together.