


2.1. Rotation Curve Decomposition. I. Technique
Consider first the rotation curve of an isothermal sphere in the ideal case where we can measure a massless disk embedded in it. Then at r << rc,
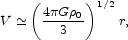 |
(1) |
and at r >> rc,
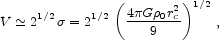 |
(2) |
where G is the gravitational constant. If we observe only the
V  r
part of the rotation curve, we can measure
r
part of the rotation curve, we can measure
 0
but not rc or
0
but not rc or
 .
Because of this,
.
Because of this,
 0 is
often the only halo parameter that we can measure
in low-luminosity galaxies. In contrast, if the measurements reach far
enough into the V = constant part of the rotation curve, then all
three parameters can be measured. Dwarf Sc - Im galaxies come closest to
the above ideal, because visible matter contributes only a small
fraction of the total mass.
0 is
often the only halo parameter that we can measure
in low-luminosity galaxies. In contrast, if the measurements reach far
enough into the V = constant part of the rotation curve, then all
three parameters can be measured. Dwarf Sc - Im galaxies come closest to
the above ideal, because visible matter contributes only a small
fraction of the total mass.
More generally, visible matter dominates the central part of the
rotation curve, and a multicomponent mass model is required.
The rotation curve of the visible matter is calculated from the
brightness distribution assuming that the mass-to-light ratio M /
L of each component is constant with radius. Values of M /
L are adjusted
to fit as much of the inner rotation curve as desired. HI gas
is taken into account separately.
Molecular gas is assumed to follow the light distribution, so it is
included in M / L. Then, given the total rotation curve
Vvis of the visible matter, the halo rotation curve is
VDM(r) = (V2 -
Vvis2)1/2. A model such as an
isothermal is then fitted to
VDM to derive the halo asymptotic velocity
V =
21/2
=
21/2  ,
rc, and
,
rc, and
 0. Rotation curve decompositions
have now been published for ~ 100 galaxies. Of these, 55 survive our
selection cuts (Section 2.3).
0. Rotation curve decompositions
have now been published for ~ 100 galaxies. Of these, 55 survive our
selection cuts (Section 2.3).