2.4. Matching Pseudo-Isothermal Models to the Isothermal Sphere

In carrying out rotation curve decompositions, some authors model the DM with a nonsingular isothermal sphere; then we adopt the parameters r_c, ₀, and without modification. Other authors use the "pseudo-isothermal sphere" (hereafter the PITS), i.e., the approximation that the volume density is

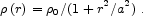(3)

They then derive parameters ₀, a, and the asymptotic circular velocity V() as r . No compelling physical argument favors one model over the other. However, if we want to combine data from different sources, we need to correct parameters determined using the PITS to the ones that would have have been measured using the isothermal. An exact correction is not possible, because equation (3) is a poor approximation to the isothermal sphere except as r . Figure 1 shows three possible scalings of the rotation and velocity dispersion curves of the PITS to the isothermal. All three scalings are shown to emphasize the physical difference between the two models. The scalings are not equally plausible, but each has a simple underlying motivation. We will find that the best scaling is intermediate between the middle and right panels of Figure 1.

Figure 1. Rotation curves (bottom) and velocity dispersion profiles (top) for the isothermal and analytic halos normalized by the velocity dispersion ITS of the isothermal sphere. The analytic halo is scaled in r and V so that both models have the same central density and (left) asymptotic rotation velocity, (middle) maximum rotation velocity, and (right) central velocity dispersion. In the bottom-right panel, the analytic and isothermal halos have similar rotation curves out to r / rc 2.5 (vertical dotted line), i.e., over the radius range of typical HI rotation curves. However, the two models extrapolate very differently as r .

At left, the PITS is scaled in r and V so that the central densities and asymptotic circular velocities are the same. Then the core radius r_c of the isothermal is r_c = 3a / 2^1/2. The dispersion scale in the top panel is the velocity dispersion of the isothermal sphere, but this is equal to the local dispersion of the PITS only as r . For most galaxies, the HI distribution does not extend beyond ~ 2.5 r_c. Here the local dispersion of the PITS is less than that of the isothermal (Fig. 1, top left). The reason is that an isotropic system with the density distribution of equation (3) is not isothermal; its velocity dispersion is

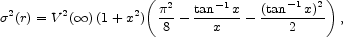(4)

where x = r / a. Since the analytic model matches the isothermal badly in both V(r) and (r), we discard this scaling.

Given the limited extent of HI data, it seems more realistic to scale the PITS so that its rotation curve is similar to that of the isothermal at r 2.5 r_c. We get such a scaling (Fig. 1, right) if we solve our problem with the halo dispersion by making the velocity dispersion of the corresponding isothermal be equal to the central dispersion (0) = (² / 8 - 1)^1/2 V() = 0.4834 V() of the PITS. Then r_c = (0.6837)3a / 2^1/2 = 1.4503 a and = 0.4834 V(). The resulting parameters are related in the normal way for an isothermal sphere, ² = 4 G ₀ r_c² / 9.

The virtue of this scaling is that the two halo rotation curves are similar over the radius range in which they are actually fitted to the data (Fig. 1, bottom right). However, there is a problem (Fig. 1, top right). This scaling forces V() to be much larger than the velocity of the flat part of the rotation curve. An examination of published decompositions shows that authors almost never extrapolate implicitly to such a large maximum rotation velocity - one that is never observed. The exceptions are some rotation curve decompositions in which V_DM r over the whole radius range of the data, i.e., cases in which r_c is completely unconstrained. Examples are the decompositions of NGC 7331 and NGC 6674 in Broeils (1992). We discard these decompositions anyway.

This suggests a compromise scaling like the one in the middle panel. Here V() is scaled to the maximum, not the asymptotic, rotation velocity of the isothermal. Then, when authors use equation (3) to derive ₀, a, and V() via rotation curve decomposition, we would adopt r_c = 1.8918 a, the authors' quoted value of ₀, and a halo velocity dispersion = 0.6306 V(). Again, these parameters are related as normal for an isothermal sphere.

In practice, there is no guarantee that any of the above scalings represents what happens when one author uses the PITS and another uses the isothermal in rotation curve decomposition. We note again that Figure 1 is included to emphasize that the PITS is not very isothermal. However, we will find in Section 3 that enough decompositions have been published using each of the above models so that we can derive the DM parameter correlations separately for each model. We will then derive the best scaling of one model to the other by matching their respective DM correlations. This scaling is used to construct Figure 4, which combines data from all sources. It is intermediate between the middle and right-hand panels of Figure 1, i.e., ₀ = 0.9255 _{0, PITS}; r_c = 1.6154 a, and = 0.7334 _PITS = 0.5186 V_{, PITS}.