


Scaling laws are new constraints on the nature of DM and on galaxy formation and evolution. Most of these remain to be explored. Simple implications include:
1 - The surprisingly high DM densities in dwarf spheroidals are normal for galaxies of such low luminosity. This implies that dSphs are real galaxies and not tidal fragments. Tides almost certainly pull bound fragments out of more luminous galaxy progenitors, but they cannot retain even the relatively low DM densities in those progenitors (Barnes & Hernquist 1992), much less increase the DM density to the high values characteristic of dwarf spheroidal galaxies.
2 - Dwarf spheroidal galaxies are not included in the
least-squares fits in Figures 2
and 4 because only
 0 can
be derived for their halos. However, these
0 can
be derived for their halos. However, these
 0
values lie on the extrapolation to low luminosity of the correlations
for spiral and irregular galaxies. That is, the DM halos of dSph and Sc
- Im galaxies appear to form a single physical sequence as a function of
DM core mass.
0
values lie on the extrapolation to low luminosity of the correlations
for spiral and irregular galaxies. That is, the DM halos of dSph and Sc
- Im galaxies appear to form a single physical sequence as a function of
DM core mass.
3 - Since virialized density depends on collapse redshift
zcoll,
 0
0
 (1 +
zcoll)3, the smallest dwarfs formed at least
(1 +
zcoll)3, the smallest dwarfs formed at least
 zcoll
zcoll  7 earlier than
the biggest spirals. Correction for baryonic DM compression will make
7 earlier than
the biggest spirals. Correction for baryonic DM compression will make
 0
smaller for giant galaxies. This will slightly
increase
0
smaller for giant galaxies. This will slightly
increase  zcoll.
zcoll.
4 - The visible matter parameters rc and
 of dSphs are a factor
of about 2 smaller than their
extrapolated DM parameters. This is reasonably consistent with the
hypothesis that extreme dSphs have low visible matter densities
(M / LB ~ 102) because they lost most
of their baryons early. Possible reasons include galactic winds (e.g.,
Dekel & Silk 1986)
or the difficulty of holding onto baryons in shallow
DM potential wells when the Universe was ionized (e.g.,
Klypin et al. 1999).
In the absence of a dark halo,
the loss of most baryons would unbind the few stars that had already
formed. But since these galaxies contain DM halos, we expect instead
that the distribution of stars has expanded to fill the halo's core.
Unlike the situation in giant galaxies, visible matter and DM would
then have similar scale parameters.
of dSphs are a factor
of about 2 smaller than their
extrapolated DM parameters. This is reasonably consistent with the
hypothesis that extreme dSphs have low visible matter densities
(M / LB ~ 102) because they lost most
of their baryons early. Possible reasons include galactic winds (e.g.,
Dekel & Silk 1986)
or the difficulty of holding onto baryons in shallow
DM potential wells when the Universe was ionized (e.g.,
Klypin et al. 1999).
In the absence of a dark halo,
the loss of most baryons would unbind the few stars that had already
formed. But since these galaxies contain DM halos, we expect instead
that the distribution of stars has expanded to fill the halo's core.
Unlike the situation in giant galaxies, visible matter and DM would
then have similar scale parameters.
5 - The fact that, as luminosity decreases, dwarf galaxies become much more numerous and also more nearly dominated by DM raises the possibility that there exists a large population of objects that are completely dark (Freeman 1987; Kormendy 1990; see also Tully 2004). Undiscovered DM dwarfs would help to solve the well known problem that the spectrum of initial density fluctuations predicted by CDM theory predicts far too many dwarf satellites of giant galaxies (Moore et al. 1999; Klypin et al. 1999). The favored explanation for why these dwarfs are not seen is that they virialized early, before or during the reionization of the Universe, and therefore lost or never captured the canonical fraction of baryons because those baryons were too hot to be confined in the puny potential wells of the dark dwarfs. Our observations suggest that empty halos - if they exist - are likely to be small and dense and to have small total masses. They would be darker versions of Draco and UMi.
6 - Djorgovski (1992)
has compared an earlier version of the DM parameter
correlations to the scaling laws predicted by hierarchical clustering
(Peebles 1974;
Gott & Rees 1975).
For a power spectrum of initial density
fluctuations that is a power law in wavenumber k,
| k|2
k|2
 kn,
the size R, density
kn,
the size R, density
 , and velocity
dispersion
, and velocity
dispersion  of a bound
object are related approximately by
of a bound
object are related approximately by
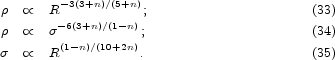 |
(33) (34) (35) |
Here we have used the relation


 2
R-2 for an isothermal
sphere. Djorgovski pointed out that the DM parameter correlations in
Kormendy (1990)
imply that n
2
R-2 for an isothermal
sphere. Djorgovski pointed out that the DM parameter correlations in
Kormendy (1990)
imply that n  -
2.45, close to the value
n
-
2.45, close to the value
n  - 2 expected
for giant galaxies in CDM theory. With the more accurate fits in equations
20 - 22,
- 2 expected
for giant galaxies in CDM theory. With the more accurate fits in equations
20 - 22,
 |
(36) (37) (38) |
we get n = - 1.80 ± 0.10,
n = - 2.12 ± 0.10, and n = - 1.81 ± 0.10,
respectively. Note that these values are not independent. Their average is
n = - 1.91. If we use the fits (equations 5 - 7) determined from
decompositions using isothermal DM, then the average is
n = - 2.1 ± 0.2. Both values are
remarkably close to the value
n  - 2.1 expected
in CDM theory at a halo mass of 1012
M
- 2.1 expected
in CDM theory at a halo mass of 1012
M (Shapiro & Iliev
2002).
We need to correct the slopes for baryonic DM compression; this will be
done in
Kormendy & Freeman
(2003).
The above comparison provides a measure of the slope of the fluctuation
power spectrum on mass scales that are smaller than those accessible to
most other methods.
(Shapiro & Iliev
2002).
We need to correct the slopes for baryonic DM compression; this will be
done in
Kormendy & Freeman
(2003).
The above comparison provides a measure of the slope of the fluctuation
power spectrum on mass scales that are smaller than those accessible to
most other methods.
Shapiro & Iliev (2002) have made a more detailed comparison of the DM parameter correlations published by Kormendy & Freeman (1996) with their predictions based on COBE-normalized CDM fluctuation spectra. They found that the agreement between predictions and observations was best for CDM.
It is interesting to note a consequence of the theoretical prediction
that the slope n gets steeper at smaller mass scales. If
n  - 2.6
for the smallest dwarfs
(Shapiro & Iliev
2002;
Ricotti 2002),
then the straight lines in the left panels of
Figure 4 should curve downward
toward the visible matter parameters of dSph galaxies. This would
strengthen the inference that the
visible and dark matter in these galaxies is distributed similarly. It will
be important to look for curvature in the correlations as more data become
available for dwarf galaxies.
- 2.6
for the smallest dwarfs
(Shapiro & Iliev
2002;
Ricotti 2002),
then the straight lines in the left panels of
Figure 4 should curve downward
toward the visible matter parameters of dSph galaxies. This would
strengthen the inference that the
visible and dark matter in these galaxies is distributed similarly. It will
be important to look for curvature in the correlations as more data become
available for dwarf galaxies.
Finally, we note that the scatter in
Figures 2 -
4 has surely been
increased by problems with the data. (1) Distance errors are not negligible.
For our calibrating galaxies, we can compare accurate distances to those
given by our Virgocentric flow field machinery. This implies errors in
logD of ± 0.11. Since
 0
0
 D-2, distance errors are a significant
- although not the dominant - source of scatter in equations 5 - 25. (2) If
some disks are submaximal, then this affects the scatter in the
correlations. If the degree to which they are submaximal depends on
MB
(Kranz, Slyz, & Rix
2003),
this affects the correlation slopes, too. (3) The assumption that
DM halos have isothermal cores is challenged by CDM theory, although it is
suppported by many observations. It will be important to see how the
correlations are affected if NFW halos are used.
(4) The correlations in Figures 2
- 4 require correction for DM
compression by the baryons before a definitive comparison with theory
can be made. We will address these issues in future papers.
D-2, distance errors are a significant
- although not the dominant - source of scatter in equations 5 - 25. (2) If
some disks are submaximal, then this affects the scatter in the
correlations. If the degree to which they are submaximal depends on
MB
(Kranz, Slyz, & Rix
2003),
this affects the correlation slopes, too. (3) The assumption that
DM halos have isothermal cores is challenged by CDM theory, although it is
suppported by many observations. It will be important to see how the
correlations are affected if NFW halos are used.
(4) The correlations in Figures 2
- 4 require correction for DM
compression by the baryons before a definitive comparison with theory
can be made. We will address these issues in future papers.
Acknowledgments
JK is grateful to the staff of Mt. Stromlo Observatory for their hospitality during three visits when part of this work was done. We thank S. Djorgovski, S. M. Fall, and P. Shapiro for helpful discussions on the comparison of predicted and observed DM scaling laws. This work used the NASA/IPAC Extragalactic Database, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with NASA.