4.2. Rotation-Dominated Pseudobulges

Figure 6, the V_max / - diagram (Illingworth 1977; Binney 1978a, b), shows that pseudobulges (filled symbols) are more rotation-dominated than classical bulges (open symbols) which are more rotation-dominated than giant ellipticals (crosses). This is disky behavior, as follows. Seen edge-on, rotation-dominated disks have parameters that approximately satisfy the extrapolation of the oblate line to 0.8. Observed other than edge-on, they project well above the oblate line. In contrast, projection keeps 0.6 isotropic spheroids near the oblate line. The filled symbols therefore represent objects that contain rapidly rotating and hence disky central components. Of the most extreme cases, NGC 4736 is discussed in detail in Kormendy & Kennicutt (2004). Complementary photometric evidence for pseudobulges in NGC 3945 and NGC 4371 is discussed in the next subsection.

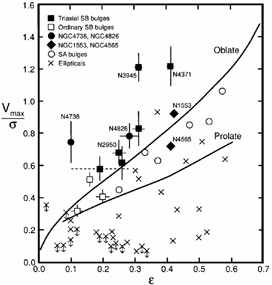Figure 6. Relative importance of rotation and velocity dispersion: Vmax / is the ratio of the maximum rotation velocity to the mean velocity dispersion interior to the half-light radius; (Vmax / )2 measures the relative contribution of ordered and random motions to the total kinetic energy and hence, via the virial theorem, to the dynamical support that gives the system its ellipticity (Binney & Tremaine 1987). The "oblate" line describes oblate spheroids that have isotropic velocity dispersions and that are flattened only by rotation. The "prolate" line is one example of how prolate spheroids can rotate more slowly for a given because they are flattened partly by velocity dispersion anisotropy. This figure is from Kormendy & Kennicutt (2004).