Annu. Rev. Astron. Astrophys. 2004. 42: 603-683 Copyright © 2004 by Annual Reviews. All rights reserved

2.2. Dynamics of Barred Galaxies: The Importance of Resonances

To understand bar-driven evolution, we need to dip briefly into the dynamics of bars. An in-depth review is provided by SW93. Here we need a primer on the nature and importance of orbital resonances.

Seen from an inertial frame, an orbit in a galactic disk is an unclosed rosette. That is, there are a nonintegral number of radial oscillations for every revolution around the center. However, in a frame of reference that rotates at the average angular velocity of the star, the star's mean position is fixed and its radial oscillation makes it move in a small ellipse around that mean position ² It is an ellipse and not just radial motion because the star revolves faster than average near pericenter and slower than average near apocenter. Any global density pattern such as a bar that rotates at the above angular velocity will pull gravitationally on the star in essentially the same way at all times and will therefore make large perturbations in its orbit. "Corotation" is the strongest of a series of resonances in which the pattern repeatedly sees the star in the same way.

For example, there is another rotating frame in which the star executes two radial oscillations for each circuit around the center. If a bar rotates at this angular velocity, it sees the stellar orbit as closed, roughly elliptical, and centered on the galactic center (Figure 4). This is called inner Lindblad resonance (ILR). It occurs when the pattern speed of the bar is _p = - / 2, where is the average angular velocity of revolution of the star and is its frequency of radial oscillation. The limit of small radial oscillations is called the epicyclic approximation; then ² = (2V / r)(V / r + dV / dr), where V(r) is the circular-orbit rotation curve (Mihalas & Routly 1968 provide a particularly transparent discussion).

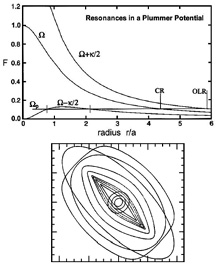Figure 4. (Top) Frequencies (r) = V(r) / r and ± / 2, where 2 = (2V / r)(V / r + dV / dr) is the epicyclic frequency of radial oscillations for almost circular orbits. This figure (Sparke & Gallagher 2000) is for a Plummer potential, but the behavior is generic. For a pattern speed p, the most important resonances occur where p = (corotation), where p = + / 2 (outer Lindblad resonance OLR) and where p = - / 2 (two inner Lindblad resonances ILR, marked with vertical dashes). (Bottom) From Englmaier & Gerhard (1997), examples of the principal orbit families for a bar oriented at 45° as in Figure 7. The elongated orbits parallel to the bar are the x1 family out of which the bar is constructed. Interior to ILR (or outer ILR, if there are two LRs), the x2 family is perpendicular to the bar. Near corotation is the 4:1 ultraharmonic resonance; the almost-square orbit makes 4 radial oscillations during each circuit around the center. Since the principal orbits change orientation by 90° at each resonance shown, they must cross near the resonances.

Resonances are important for several reasons. Figure 4 shows generic frequency curves and the most important periodic orbit families in a barred galaxy. We can begin to understand how a self-consistent bar is constructed by exploiting the fact that - / 2 varies only slowly with radius (except near the center, if there is an ILR). Calculations of orbits in a barred potential show that the main "x₁" family of orbits is elongated parallel to the bar between ILR and corotation. Bars are largely made of x₁ orbits and similar, non-periodic orbits that are trapped around them by the bar's self-gravity. Typical x₁ orbits are shown in the bottom panel of Figure 4. They are not nearly circular, but the essence of their behavior is captured if we retain the language of the epicyclic approximation and say that orbits of different radii look closed in frames that rotate at different angular velocities - / 2. But if - / 2 varies only a little with radius,

then it is possible to pick a single pattern speed _p in which the orbits precess almost together. If they precessed exactly together, then one could make a bar by aligning elongated orbits as in the bottom panel of the figure. Since - / 2 is not quite constant, it is the job of self-gravity to make the orbits precess not approximately but exactly together. This idea was used to understand self-consistent bars by Lynden-Bell & Kalnajs (1972) and by Lynden-Bell (1979) and to demystify spiral structure by Kalnajs (1973) and by Toomre (1977b). They were following in the pioneering footsteps of Bertil Lindblad (1958, 1959: see Section 20).

Calculations of orbits in barred potentials reveal other orbit families (e.g., Contopolous & Mertzanides 1977; Athanassoula 1992a, b; SW93), only a few of which are relevant here. Next in importance is the x₂ family, which lives interior to ILR and which is oriented perpendicular to the bar (Figure 4, bottom). Between corotation and OLR, the principal orbits are elongated perpendicular to the bar, and outside OLR, they are again oriented parallel to the bar. Near corotation is the 4:1 ultraharmonic resonance in which a star executes 4 radial oscillations for every revolution: _p = - / 4. We will need these results in the following sections.

The important consequence is emphasized by Sellwood & Wilkinson (1993): "Not only do the eccentricities of the orbits increase as exact resonance is approached, but the major axes switch orientation across all three principal resonances, making the crossing of orbits from opposite sides of a resonance inevitable" (bottom panel of Figure 4). This is important mainly when the orbits are very noncircular, as in strongly barred galaxies. Now, orbits that cross are no problem for stars. But gas clouds that move on such orbits must collide near resonances. Dissipation is inevitable, and the consequence is an increase in the gas density and hence star formation. This heuristic discussion helps to explain the numerical results reviewed in the following sections, in which gas tends to build up in rings and to form stars there.

² It is an ellipse and not just radial motion because the star revolves faster than average near pericenter and slower than average near apocenter. Back.