Copyright © 2004 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2004. 42:
603-683 Copyright © 2004 by Annual Reviews. All rights reserved |
4.10. In Which Pseudobulges Fade Out Into Disks
Böker, Stanek, & van der Marel (2003) investigate how pseudobulges fade out into disks. Their most subtle examples of pseudobulges also highlight fundamental uncertainties about the meaning of profile decomposition. M 33 (Figure 19) provides an example. The disk has somewhat irregular but global-pattern spiral structure (Sandage 1961; Sandage & Bedke 1994). There is no sign of an ILR, i.e., the spiral arms become radial near the center and pass through it. At the center, a very distinct nucleus (Kormendy & McClure 1993) is representative of the ones discussed in Section 4.9. Figure 19 shows that the disk surface brightness profile has a subtly two-component look; it is well fitted by the sum of two exponentials. The figure shows a decomposition into a Sérsic function plus an outer exponential; it confirms that n = 1.09 ± 0.18 for the inner component. This inner component is essentially the "bulge" discussed by Minniti, Olszewski, & Rieke (1993). It is also visible as a subtle upturn in surface brightness at r < 150" in the JHK profiles posted at the 2MASS web site. What does this mean? Does M 33 contain a pseudobulge?
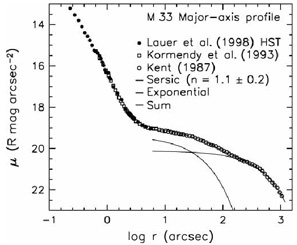 |
Figure 19. Major-axis surface brightness profile of M 33. The steep rise in surface brightness near the center is the nucleus. The rest of the profile has been decomposed into an inner Sérsic function plus an exponential. We thank S. Faber and the Nuker team for suggesting a discussion of M 33. |
The inner component is consistent with, although on the low-density side of, the parameter distribution for "exponential bulges" given in Carollo (1999). The effective radius of the inner component is re = 0.31 ± 0.05 kpc, and the mean surface brightness within re is 20.7 ± 0.2 R mag arcsec-2. (All errors quoted take account of parameter coupling in the decomposition.) If one applies profile decomposition in the canonical way, then one could reasonably conclude that this is a pseudobulge not unlike the fluffiest ones discussed in the literature.
On the other hand, we are uneasy about the decomposition in
Figure 19.
The distinction between the components is subtle. The inner one is at
most a factor of 2 brighter than the outer one, and it is so only at
r < 10" where the outer exponential has already been
extrapolated
far inward. The stars in both components are presumably in nearly circular
orbits; stars that define the outer exponential do not, by and large,
visit the inner exponential and vice versa. Does it really make sense to
say that half of the disk stars at
r  25"
belong to the main disk and half
belong to a pseudobulge? If we could observe each star, how would we decide
which ones belong to the bulge and which to the
disk? It is difficult to believe, given substantial spread in kinematic and
composition properties, that there would be such a clean separation into two
components that we could label each star correctly. Another way to put it is
this: Since the fitting functions used for each component are not physically
motivated or explained, is there any reason to believe that each one
extrapolates without change into the part of the galaxy that is
dominated by the other? And still another way: No theory of the
formation of exponential disks explains why an exponential is so magic
and so required that modest departures from it cry out for
explanation. We already accept
Freeman (1970a)
"Type II" profiles as canonical disk behavior, even though we can
explain it in only a few cases (e.g.,
Talbot, Jensen, &
Dufour 1979).
We accept outer cutoffs (e.g.,
van der Kruit &
Searle 1981a,
b;
1982).
Oval disks are only piecewise exponential
(Section 3.2). Would it be a surprise if
disks also knew how to deviate above an inward extrapolation to small radii?
25"
belong to the main disk and half
belong to a pseudobulge? If we could observe each star, how would we decide
which ones belong to the bulge and which to the
disk? It is difficult to believe, given substantial spread in kinematic and
composition properties, that there would be such a clean separation into two
components that we could label each star correctly. Another way to put it is
this: Since the fitting functions used for each component are not physically
motivated or explained, is there any reason to believe that each one
extrapolates without change into the part of the galaxy that is
dominated by the other? And still another way: No theory of the
formation of exponential disks explains why an exponential is so magic
and so required that modest departures from it cry out for
explanation. We already accept
Freeman (1970a)
"Type II" profiles as canonical disk behavior, even though we can
explain it in only a few cases (e.g.,
Talbot, Jensen, &
Dufour 1979).
We accept outer cutoffs (e.g.,
van der Kruit &
Searle 1981a,
b;
1982).
Oval disks are only piecewise exponential
(Section 3.2). Would it be a surprise if
disks also knew how to deviate above an inward extrapolation to small radii?
We believe that it is not possible, given the available information, to distinguish between the following possibilities: It is entirely plausible that the inner exponential is a protopseudobulge. Alternatively, disk profiles can have a variety of wiggles and this is one of them. Interestingly, the inner component is significant out to a radius that is comparable to the width of the spiral arms. Spiral arms pass through the center when there is no ILR. This means that the profile near the center measures light only from a spiral arm crest, while the profile farther out is an average over arm crests and arm troughs. This could be part of the explanation of the "inner component".
This discussion highlights a fundamental conceptual uncertaintly with the blind application of profile decompostion. In the case of a big, classical bulge plus an obvious disk, we can be confident that a decomposition has physical meaning. We know this from edge-on galaxies. The bulge in the Sombrero galaxy clearly extends into and beyond the radii where we would see the disk if the galaxy were face-on; at these radii, we would see bulge stars in front of and behind the disk. Bulge formation via mergers guarantees that this be so, because some stars in a merger always splash out to large radii. But secular evolution involves the slow transport of gas that is never far from dynamical equilibrium. No substantial splashing occurs. The concept that a pseudobulge coexists, at some radius of interest, with a disk that was already in place has much less physical meaning than it does in the case of a classical bulge. It is not clear to us that decomposition has any meaning at all in distinguishing pseudobulges from disks. It may be more meaningful to fit the profile piecewise.
Decomposition remains a useful way to derive diagnostic parameters. We should not overinterpret the results. Further work is needed to define the boundaries between what deserves interpretation and what does not.
What are the implications? We believe that the conclusions about well developed pseudobulges - the ones whose profiles rise well above the inward extrapolation of the disk profile, as in Figures 10 to 12 - are unchanged. The Fundamental Plane correlations then tell us that the dividing line between pseudobulges and disks is just as fuzzy as the one between classical bulges and pseudobulges. The reason is not that our machinery is inadequate. The reason is that there is a physical continuum between disks and pseudobulges, as suggested by Kormendy (1993) and by Böker, Stanek, & van der Marel (2003c). The sequence of pseudobulges fades out not where they become tiny, like nuclei, but where they become large, low in surface brightness, and indistinguishable from disks.