Copyright © 2004 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2004. 42:
603-683 Copyright © 2004 by Annual Reviews. All rights reserved |
4.6. "Bulges" With The Dynamics of Disks: The V /
 -
-
 Diagram
Diagram
Figure 17, the Vmax /
 -
-
 diagram
(Illingworth 1977;
Binney 1978a,
b),
shows that pseudobulges (filled symbols) are more
rotation-dominated than classical bulges (open circles), which are more
rotation-dominated than giant elliptical galaxies (crosses). This is disky
behavior.
diagram
(Illingworth 1977;
Binney 1978a,
b),
shows that pseudobulges (filled symbols) are more
rotation-dominated than classical bulges (open circles), which are more
rotation-dominated than giant elliptical galaxies (crosses). This is disky
behavior.
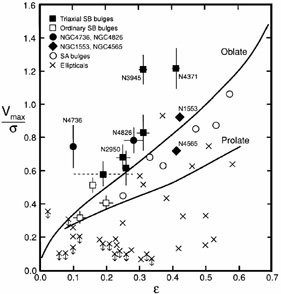 |
Figure 17. The relative dynamical
importance of rotation and random motions as a function of observed
ellipticity for various kinds of stellar systems. Here
Vmax / |
The essential features of the
Vmax /  -
-  diagram
are as follows:
diagram
are as follows:
The virial theorem relates the gravitational
potential and kinetic
energy tensors; the former involves the shape of the stellar system; the
latter involves the balance between rotational and random
kinetic energies
(Binney 1978a;
Binney & Tremaine
1987).
In Figure 17, Vmax /
 is a surrogate for the
(square root of) the ratio of ordered to random kinetic energies and
is a surrogate for the
(square root of) the ratio of ordered to random kinetic energies and
 is the apparent
flattening.
is the apparent
flattening.
If rotation is dynamically unimportant
(Vmax /
 << 1) and
if the system is flattened, then it must be anisotropic
(Binney 1976;
1978a,
b;
1980;
1982).
Stars climb farthest out of their mutual gravitational potential
well in the direction in which the velocity dispersion is largest.
<< 1) and
if the system is flattened, then it must be anisotropic
(Binney 1976;
1978a,
b;
1980;
1982).
Stars climb farthest out of their mutual gravitational potential
well in the direction in which the velocity dispersion is largest.
Rotation adds extra flattening regardless of
velocity anisotropy, because rotation plus random motions allow stars to
climb farther out of their
mutual gravitational potential well than do random motions alone. Isotropic
systems that are flattened into spheroids by rotation have a simple
relationship between flattening and Vmax /
 that is shown by the
"oblate" line in Figure 17.
Binney (1978a)
gives it implicitly;
Fall (1981)
provides an explicit equation for the projected configurataion seen
edge-on, and
Kormendy (1982a)
gives an approximation formula, Vmax /
that is shown by the
"oblate" line in Figure 17.
Binney (1978a)
gives it implicitly;
Fall (1981)
provides an explicit equation for the projected configurataion seen
edge-on, and
Kormendy (1982a)
gives an approximation formula, Vmax /

 [
[ / (1 -
/ (1 -
 )]1/2,
that is good to 1 % for 0
)]1/2,
that is good to 1 % for 0 

 0.95.
0.95.
For 0.1


 0.5, projection
moves an isotropic oblate spheroid almost parallel to the oblate
line. If an isotropic spheroid with
0.5, projection
moves an isotropic oblate spheroid almost parallel to the oblate
line. If an isotropic spheroid with
 = 0.5 is seen at a
skew orientation so that it looks like an
= 0.5 is seen at a
skew orientation so that it looks like an
 = 0.3 system seen
edge-on, then both sustems have approximately the same value of
Vmax /
= 0.3 system seen
edge-on, then both sustems have approximately the same value of
Vmax /  .
However, an edge-on disk that is near the oblate line at
.
However, an edge-on disk that is near the oblate line at
 ~ 0.9 ± 0.1
projects well above the oblate line when it is seen other than edge-on.
~ 0.9 ± 0.1
projects well above the oblate line when it is seen other than edge-on.
Observations show that most giant ellipticals have insignificant rotation and are dominated by velocity anisotropy (Bertola & Capaccioli 1975; Illingworth 1977; crosses in Figure 17). Low-luminosity ellipticals are more nearly isotropic and consistent with the oblate line (Davies et al. 1983). And classical bulges are consistent with being isotropic oblate rotators (Illingworth & Schechter 1982; Kormendy & Illingworth 1982; Kormendy 1982b; open circles in Figure 17). Classical bulges fall slightly to the right of the oblate line, but the extra flattening is provided by the disk potential (Jarvis & Freeman 1985).
The above papers show that anisotropic giant ellipticals are triaxial. We emphasize that this triaxiality is different from that of bars. Ellipticals are triaxial because they have little angular momentum. They are made largely out of "box orbits" that have no net angular momentum (see Binney & Tremaine 1987 for discussion). Rotation is provided by "z-axis tube orbits" that encircle the z = rotation axis; in a triaxial elliptical, these are somewhat elongated in the direction of the longest axis. Other orbits, including chaotic ones, are present as well. But the essential character of an elliptical is defined by its box orbits.
In contrast, a barred galaxy is barred not because it has little angular momentum but rather because it has too much for the combination of its velocity dispersion and its central concentration. This is why the disk made a bar. Bars are not made of box orbits; they are made of x1 orbits. These are very elongated z-axis tubes that, in some cases, include baroque decorations such as loops. They have lots of angular momentum.
It is important to keep in mind the distinction between bars and ellipticals. They are not different versions of each other, and they virtually never occur together. A bar is fundamentally a disk phenomenon.
Contrast the behavior of the bulges that are plotted in Figure 17 as filled symbols. They are above the oblate line and even more above the distribution of classical bulges (open symbols). Rotation is more important in these objects than it is in classical bulges and ellipticals. Point 4, above, shows why this is disk-like behavior. It indicates an admixture of stars that are flattened, dynamically cold, and rapidly revolving around the galactic center - that is, a disk contribution that would appear near the oblate line if seen edge-on but that plots well above the oblate line at the skew inclinations of these galaxies. The filled symbols include barred galaxies and the prototypical unbarred oval galaxy NGC 4736 (Figures 2 and 8). Another prominent example is NGC 3945; its rapidly rotating "bulge" is the nuclear bar shown in Figure 14 (see also Erwin et al. 2003 for a detailed discussion). Another is NGC 2950, also a nuclear bar. Thus the dynamical evidence agrees with other evidence that these are pseudobulges.
Two pseudobulges from
Kormendy &
Illingworth (1982)
deserve comment (filled diamonds in Figure 17).
NGC 1553 contains a
prototypical lens in an unbarred galaxy (point 7
of Section 2.1).
Figure 17 shows that it has an unusually high
value of (Vmax /
 )*
for an unbarred galaxy. Consistent with the suggestion
that the lens is a defunct bar
(Kormendy 1979b,
1984)
(Section 3.3),
the hint is that the galaxy grew a pseudobulge while it was still barred.
In contrast, the boxy bulge of NGC 4565 has (Vmax /
)*
for an unbarred galaxy. Consistent with the suggestion
that the lens is a defunct bar
(Kormendy 1979b,
1984)
(Section 3.3),
the hint is that the galaxy grew a pseudobulge while it was still barred.
In contrast, the boxy bulge of NGC 4565 has (Vmax /
 )* =
0.86 ± 0.16. This is smaller than (Vmax /
)* =
0.86 ± 0.16. This is smaller than (Vmax /
 )*
values for other pseudobulges. However, a box-shaped pseudobulge rotates
cylindrically, so (Vmax /
)*
values for other pseudobulges. However, a box-shaped pseudobulge rotates
cylindrically, so (Vmax /
 )*
underestimates the dynamical importance of rotational kinetic energy
compared with ellipsoidal bulges.
)*
underestimates the dynamical importance of rotational kinetic energy
compared with ellipsoidal bulges.
The difference between classical and pseudobulges need not always be
large. It is entirely implausible that secular evolution sometimes
augments a classical bulge with new, disky material. We also point out in
Section 7.1 that pseudobulges can
heat themselves in the vertical direction, thereby decreasing their
dynamical difference from classical bulges. Therefore, large
(Vmax /
 ) is
evidence for a pseudobulge, but values comparable to those on the oblate
line do not guarantee that the bulge is classical.
) is
evidence for a pseudobulge, but values comparable to those on the oblate
line do not guarantee that the bulge is classical.