4. MODELS WHICH ACCOUNT FOR THE ENTIRE OPTICAL/FIR/SUBMM SEDs

The challenge of models which account for the entire optical/FIR/submm SEDs is to identify an intrinsic distribution of stars and dust which is consistent with the observed integrated SEDs and surface brightness distributions, both in the optical and FIR/submm ranges. In addition to the radiative transfer code, such models should also incorporate a technique to calculate the dust emission, as outlined below:

For a given spatial distribution of stars and dust, we can calculate the energy densities u at each position in the galaxy through a radiative transfer calculation, which needs to take into account both absorption and scattering. Then, for a given grain model (which in this context means a given grain absorption/emission efficiency Q_abs) and a given distribution N(a) in (spherical) grain size a, the energy balance between emission and absorption is given in terms of a probability distribution P(a, T) in the temperature T of each grain by the following equation:

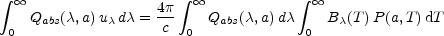Having solved for P(a, T) (see for example Guhathakurta & Draine [26]), the dust emission F can be calculated at each position in a galaxy at distance d using:

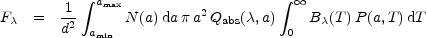where a_min and a_max are the minimum and maximum grain sizes present in the distribution.

A probability distribution of temperatures arises because grains are impulsively heated by photons. Only when the typical interval between photon hits is much shorter than the timescale for the energy deposited in each photon hit to be radiated does the probability distribution tend towards a delta function - the case of grains emitting at their equilibrium temperature. In general grains smaller than a certain critical size (depending on the strength and colour of the radiation field and composition of the grain) emit stochastically, and grains bigger than this critical size emit at equilibrium temperature. As the radiation fields are increased, grains of progressively smaller sizes radiate at equilibrium temperature. Conversely, as radiation fields are decreased, grains of progressively larger sizes will radiate stochastically. These trends are illustrated in Fig. 2.

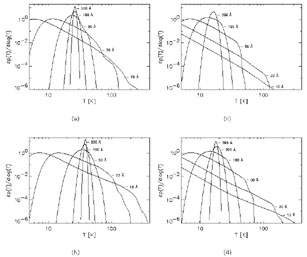Figure 2. Examples of temperature distribution for spherical dust grains (with radii 10, 20, 50, 100, 200, & 398Å) embedded in the diffuse radiation field of NGC 891, taken from Popescu et al. [46]: a) silicate grains in the centre of the galaxy (R = 0 kpc, z = 0 kpc); b) graphite grains in the centre of the galaxy; c) silicate grains at the edge of the galactic disk (R = 15 kpc, z = 0 kpc); d) graphite grains at the edge of the galactic disk.