


Traditionally, the effect of dust in attenuating stellar light in galaxies has been quantified purely empirically by statistical analysis of the variation of optical surface brightness with inclination. However, this variation is small in comparison with the scatter, so that this method is not useful for estimating the attenuation of light in individual galaxies. For this reason, there has always been a strong incentive to develop models for the attenuation of stellar light in galaxies. With the development of radiative transfer calculations on high speed computers, such models have become a practical possibility. The problem, however, has been to identify realistic geometries for stars and dust, since, as demonstrated in this review, these are not well constrained by optical data alone. Consequently, until very recently, models for attenuation have largely concentrated on evaluating the effect different choices for the geometries of stars and dust would have on the attenuation. The geometry was varied to investigate the effect of the inclusion or non-inclusion of different structures, such as clumps or bulges, as well as simply to investigate the effects of varying the parameters of structures, such as scalelengths and scaleheights of disks of dust and stars.
This type of work was done by Bianchi [8], Ferrara et al. [18], Baes & Dejonghe [2] and Pierini et al. [42]. For example Ferrara et al. provided an atlas of dust attenuation calculated as a function of geometry, inclination, dust optical depth, and extinction properties. This atlas is available in electronic format. As an application they compared the predicted variation of apparent magnitude with inclination with the observed one. Pierini et al. [42] investigated the effect of the dust being distributed in "passive" clumps (as defined in Sect. 5), rather than homogeneously. In this work the large scale distributions of stars and dust and the dust-type were fixed, and the attenuation characteristics of the bulge and disk as seen through the whole distribution of dust were calculated separately.
The recent development of models which reproduce the observed optical/FIR/submm SEDs and the surface brightness distributions in both optical and FIR range means that the geometry of stars and dust is no longer a free choice, but should conform to the solution adopted by these models. Such an approach was taken by Tuffs et al. [53], who used the SED model of Popescu et al. [46] to calculate the attenuation of stellar light in spiral galaxies. Unlike previous studies of attenuation, this model incorporates a second disk of dust and "active" clumps. These new elements affect both the inclination and wavelength dependence of attenuation. In order to make the model applicable to a wide range of bulge-to-disk ratios and degrees of clumpiness, separate calculations were done for the main stellar components: older stellar disk, young stellar disk and bulge, each seen through two dust disks, while the clumpy component was treated analytically. In Fig. 15 we show examples of attenuation curves taken from Tuffs et al. [53]. For all geometrical components there is an obvious increase in attenuation with increasing inclination, with the exception of the attenuation of the bulge when the inclination approaches the edge-on view. Also, the increase in attenuation with increasing inclination is stronger for larger face-on opacities than for lower ones, irrespective of geometry or wavelength. These solutions of attenuation as a function of inclination, opacity and wavelength are available in electronic format for general use by the community. These data can be used to construct attenuation curves for any combination of bulge-to-disk ratio and clumpiness factor. The effect of varying the bulge-to-disk ratio is one of the most important factors in shaping the attenuation curves in the optical/NIR range. In general, ignoring the presence of bulges can lead to a systematic overestimate of the opacity of disks. Also the effect of varying the clumpiness factor is one of the most important factors in shaping the attenuation curves in the UV range.
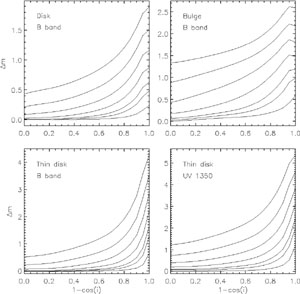 |
Figure 15. Examples taken from Tuffs et al.
[53]
of the dependence of attenuation
( |