Copyright © 2002 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 2002. 40:
539-577 Copyright © 2002 by Annual Reviews. All rights reserved |
Galaxy clusters arise from the gravitational collapse of rare high
peaks of primordial density perturbations in the hierarchical
clustering scenario for the formation of cosmic structures
(e.g. Peebles 1993,
Coles & Lucchin 1995,
Peacock 1999).
They probe
the high-density tail of the cosmic density field and their number
density is highly sensitive to specific cosmological scenarios (e.g.
Press & Schechter
1974,
Kofman et al. 1993,
Bahcall & Cen 1993,
White et al. 1993a).
The space density of clusters in the local
universe has been used to measure the amplitude of density
perturbations on ~ 10 Mpc scales. Its evolution, which is
driven by the growth rate of density fluctuations, essentially depends
on the value of the matter density parameter
m
1 (e.g.
Oukbir & Blanchard
1992,
Eke et al. 1998,
Bahcall et al. 1999).
Figure 1 shows how structure formation
proceeds and the cluster population evolves in two
cosmological models, characterized by different values of
m. High
and low density universes show largely different
evolutionary patterns, which demonstrate how the space density of
distant clusters can be used as a powerful cosmological diagnostic.
What cosmological models actually predict is the number density of
clusters of a given mass at varying redshifts. The cluster mass,
however, is never a directly observable quantity, although several
methods exist to estimate it from observations.
 |
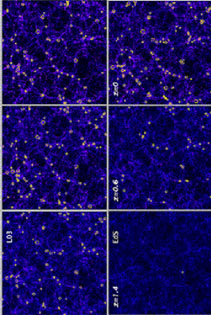Figure 1. The evolution of the cluster
population from N-body simulations in two different cosmologies (from
Borgani & Guzzo
2001).
Left panels describe a flat, low-density model with
|
Determining the evolution of the space density of clusters requires counting the number of clusters of a given mass per unit volume at different redshifts. Therefore, three essential tools are required for its application as a cosmological test: i) an efficient method to find clusters over a wide redshift range; ii) an observable estimator of the cluster mass and iii) a method to compute the selection function or equivalently the survey volume within which clusters are found.
Clusters form via the collapse of cosmic matter over a region of
several megaparsecs. Cosmic baryons, which represent approximately
10-15% of the mass content of the Universe, follow the dynamically
dominant dark matter during the collapse. As a result of adiabatic
compression and of shocks generated by supersonic motions during shell
crossing and virialization, a thin hot gas permeating the cluster
gravitational potential well is formed. For a typical cluster mass of
1014-1015
M
this
gas reaches temperatures of several
107 K, becomes fully ionized and, therefore, emits via thermal
bremsstrahlung in the X-ray band.
Observations of clusters in the X-ray band provide an efficient and physically motivated method of identification, which fulfills the three requirements above. The X-ray luminosity, which uniquely specifies the cluster selection, is also a good probe of the depth of the cluster gravitational potential. For these reasons most of the cosmological studies based on clusters have used X-ray selected samples. X-ray studies of galaxy clusters provide: (1) an efficient way of mapping the overall structure and evolution of the Universe and (2) an invaluable means of understanding their internal structure and the overall history of cosmic baryons.
X-ray cluster studies made substantial progress at the beginning of the 90s with the advent of new X-ray missions. Firstly, the all-sky survey and the deep pointed observations conducted by the ROSAT satellite have been a goldmine for the discovery of hundreds of new clusters in the nearby and distant Universe. Follow-up studies with ASCA and Beppo-SAX satellites revealed hints of the complex physics governing the intra-cluster gas. In addition to gas heating associated with gravitational processes, star formation processes and energy feedback from supernovae and galactic nuclear activity are now understood to play an important role in determining the thermal history of the intra-cluster medium (ICM), its X-ray properties and its chemical composition. Studies utilizing the current new generation of X-ray satellites, Chandra and Newton-XMM, are radically changing our X-ray view of clusters. The large collecting area of Newton-XMM, combined with the superb angular resolution of Chandra, have started to unveil the interplay between the complex physics of the hot ICM and detailed processes of star formation associated with cool baryons.
The aim of this article is to provide an up-to-date review on the methodology used to construct X-ray selected cluster samples and to investigate their evolutionary properties. We emphasize the evolution of the space density of clusters and their physical parameters. Additional reviews on galaxy clusters include: Forman & Jones (1982) and Sarazin (1988) for historical reviews on X-ray properties of galaxy clusters; Bahcall (1988) and Borgani & Guzzo (2001) for large-scale structure studies of galaxy clusters; Fabian (1994) for the physics of cooling flows in clusters; Mulchaey (2000) for the X-ray properties of galaxy groups; Birkinshaw (1999) and Carlstrom et al. (2001) for cluster studies with the Sunyaev-Zeldovich effect; Mellier (1999) for studies of the mass distribution of clusters via gravitational lensing and van Dokkum & Franx (2001) for the study of galaxy populations in clusters.
1 The
matter-density parameter is defined as
m =
/
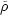c,
where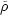
is the cosmic mean matter density;
c =
1.88 10-29 h2 g cm-3 is the
critical density; h and h50 denote the Hubble
constant H0 respectively in units of
100 and 50 km s-1 Mpc-1.
is
referred to as
the contribution to the total mass-energy density of the Universe
associated with the cosmological constant
.
Back.