3. COSMOLOGICAL PARAMETERS

The current `Standard Model' of cosmology contains around 10 free parameters (see Cosmological Parameters' mini-review [12]). The basic framework is the Friedmann-Robertson-Walker metric (i.e., a universe that is approximately homogeneous and isotropic on large scales), with density perturbations laid down at early times and evolving into today's structures (see `Big-Bang Cosmology' mini-review [13]). These perturbations can be either `adiabatic' (meaning that there is no change to the entropy per particle for each species, i.e., / for matter is (3/4) / for radiation) or `isocurvature' (meaning that, for example, matter perturbations compensate radiation perturbations so that the total energy density remains unperturbed, i.e., for matter is - for radiation). These different modes give rise to distinct phases during growth, and the adiabatic scenario is strongly preferred by the data. Models that generate mainly isocurvature type perturbations (such as most topological defect scenarios) are no longer considered to be viable.

Within the adiabatic family of models, there, is in principle, a free function describing how the comoving curvature perturbations, , vary with scale. In inflationary models, the Taylor series expansion of ln(ln k) has terms of steadily decreasing size. For the simplest models, there are thus 2 parameters describing the initial conditions for density perturbations: the amplitude and slope of the power spectrum, <||²> kⁿ. This can be explicitly defined, for example, through:

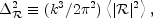and using A^{2 2}(k₀) with k₀ = 0.05 Mpc^-1. There are many other equally valid definitions of the amplitude parameter (see also Refs. [12] and [13]), and we caution that the relationships between some of them can be cosmology dependent. In `slow roll' inflationary models this normalization is proportional to the combination V³ / (V')², for the inflationary potential V(). The slope n also involves V", and so the combination of A and n can, in principle, constrain potentials.

Inflationary models can generate tensor (gravity wave) modes as well as scalar (density perturbation) modes. This fact introduces another parameter measuring the amplitude of a possible tensor component, or equivalently the ratio of the tensor to scalar contributions. The tensor amplitude A_T V, and thus one expects a larger gravity wave contribution in models where inflation happens at higher energies. The tensor power spectrum also has a slope, often denoted n_T, but since this seems likely to be extremely hard to measure, it is sufficient for now to focus only on the amplitude of the gravity wave component. It is most common to define the tensor contribution through r, the ratio of tensor to scalar perturbation spectra at large scales (say k = 0.002 Mpc^-1). There are other definitions in terms of the ratio of contributions to C₂, for example. Different inflationary potentials will lead to different predictions, e.g. for ⁴ inflation, r = 0.32, while other models can have arbitrarily small values of r. In any case, whatever the specific definition, and whether they come from inflation or something else, the `initial conditions' give rise to a minimum of 3 parameters: A, n and r.

The background cosmology requires an expansion parameter (the Hubble Constant, H₀, often represented through H₀ = 100 h km s^-1 Mpc^-1) and several parameters to describe the matter and energy content of the Universe. These are usually given in terms of the critical density, i.e., for species `x', _x = _x / _crit, where _crit = 3H₀² / 8 G. Since physical densities _{x x} h² _x are what govern the physics of the CMB anisotropies, it is these s that are best constrained by CMB data. In particular CMB observations constrain _B h² for baryons and _M h² for baryons plus Cold Dark Matter.

The contribution of a cosmological constant (or other form of Dark Energy) is usually included through a parameter which quantifies the curvature, _K 1 - _tot, where _tot = _M + . The radiation content, while in principle a free parameter, is precisely enough determined through the measurement of T.

The main effect of astrophysical processes on the Cs comes through reionization. The Universe became reionized at some redshift long after recombination, affecting the CMB through the integrated Thomson scattering optical depth:

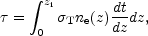where _T is the Thomson cross-section, n_e(z) is the number density of free electrons (which depends on astrophysics) and dt / dz is fixed by the background cosmology. In principle, can be determined from the small scale power spectrum together with the physics of structure formation and feedback processes. However, this is a sufficiently complicated calculation that needs to be considered as a free parameter.

Thus we have 8 basic cosmological parameters: A, n, r, h, _B h², _M h², _tot, and . One can add additional parameters to this list, particularly when using the CMB in combination with other data sets. The next most relevant ones might be: h², the massive neutrino contribution; w ( p / ), the equation of state parameter for the Dark Energy; and dn / d ln k, measuring deviations from a constant spectral index. To these 11 one could of course add further parameters describing additional physics, such as details of the reionization process, features in the initial power spectrum, a sub-dominant contribution of isocurvature modes, etc.

As well as these underlying parameters, there are other quantities that can be derived from them. Such quantities include the actual s of the various components (e.g., _M), the variance of density perturbations at particular scales (e.g., ₈), the age of the Universe today (t₀), the age of the Universe at recombination, reionization, etc.