


In Figure 2, I present four LFs from my earlier work [38 - 41]. Other published LFs (in addition to the ones already listed) are presented in references 12, 19, 20, 33, 34, and 47.
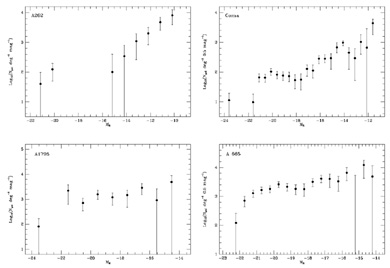 |
Figure 2. The R-band luminosity
functions of A 262 (z = 0.016), Coma (z = 0.023), A 1795 (z = 0.063), and A 665
(z = 0.182). In converting apparent to absolute magnitudes,
I assume H0 = 75 km s-1 Mpc-1 and
|
For A 262 (a poor cluster at z = 0.016), signs of a turn-up at the faint-end (MR < - 14) are seen, but the LF is not well-constrained at bright magnitudes here because the galaxy density is too low. In Coma, a richer cluster at approximately the same distance as A 262, a similar turn-up at the faint-end is seen, but a far more shallow LF is observed at brighter magnitudes. In both cases, the statistics are poor at the faint-end because the field-to-field variance of the background is so large - nevertheless, in both cases the turn-up at the faint-end is statistically significant and the LF is not fit by either a power-law or a Schechter function [30] over the entire range -20 < MR < - 11). For the more distant clusters, A 1795 and A 665, a flatter LF is seen but the very faint magnitudes at which the turn-up is seen in A 262 and Coma are not probed in these clusters.
The approximate similarity of the form of the LFs in the four clusters in Figure 2 suggests that it might be productive to combine the individual cluster LFs in order to improve the statistics. This is done in Figure 3. When performing this calculation, I found that each individual cluster LF is consistent with the composite LF to a high degree of statistical significance. This is suggestive that the LF of galaxies in the cores of rich clusters is remarkably constant. Also, the Fornax LF of Ferguson [10] is also consistent with this composite function at a high level of significance down to MB = - 13 (see ref. 42 - this is particularly intriguing because the errors in the Fornax sample at the faint end come only from counting statistics and are quite small).
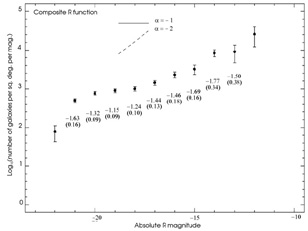 |
Figure 3. Composite R-band
luminosity function of rich clusters (derived using the LFs from Coma, A 2199, A 1795,
A 1146, A 665, and A 963). This represents the weighted average of
the individual LFs, normalized to a projected galaxy density corresponding
to that of a typical Abell richness 2 cluster. Local values of
|
The composite LF in Figure 3 has much better
statistics than the LFs
shown in Figure 2, now that a sample of clusters
have been combined. The composite LF shows the following properties:
1) the LF shows significant curvature at both the bright and faint-ends.
Neither a power-law nor Schechter function
[30]
provides a good fit to the data.
A similar conclusion was made for the Coma LF in
Figure 2, but the
smaller error bars in Figure 3 now make this
true at a far higher level of confidence.
2) at no magnitude is
 = - 1 a good fit to the
data. We note however the peculiar result that the LF is flattest
(
= - 1 a good fit to the
data. We note however the peculiar result that the LF is flattest
( = - 1.2) at about
MR = - 19, which is the transition magnitude
between giants ellipticals and dwarfs in the Binggeli diagram (most giant
galaxies in the centers of rich clusters are ellipticals).
This is suggestive of a conspiracy in which the giant galaxy LF is falling
by an amount almost exactly compensated for by the rise in the dwarf
galaxy LF at MR = - 19).
= - 1.2) at about
MR = - 19, which is the transition magnitude
between giants ellipticals and dwarfs in the Binggeli diagram (most giant
galaxies in the centers of rich clusters are ellipticals).
This is suggestive of a conspiracy in which the giant galaxy LF is falling
by an amount almost exactly compensated for by the rise in the dwarf
galaxy LF at MR = - 19).
3) the turn-up at the faint-end appears to be very steep. The new
results for Virgo (ref.
27,
Jones et al. these proceedings) suggest a value
of  = - 2.1 at
MR = - 12. The statistics that Phillipps, Jones
and collaborators got for Virgo are significantly better than I show
for A 262 or Coma in Figure 2, because in Virgo
a background subtraction is not required.
= - 2.1 at
MR = - 12. The statistics that Phillipps, Jones
and collaborators got for Virgo are significantly better than I show
for A 262 or Coma in Figure 2, because in Virgo
a background subtraction is not required.
On theoretical grounds, this steep LF is not predicted to extend to
indefinitely faint magnitudes because we expect photoionization from the
UV background to suppress the conversion of gas into stars in very low mass
systems [36].
On observational grounds, we arrive
at the same prediction from the requirement that the integrated light from
small galaxies not overproduce the measured intracluster light
(see Section 8 below). It is, however,
interesting to note that between
about MR = - 13 and whenever this turnover occurs, the
LF has approximately the same shape
( ~ - 2)
as the mass function predicted
[49]
from Press-Schechter theory (i.e. if Press-Schechter theory is valid in this
context, then over this magnitude
range, the combined efficiency of all the baryonic processes which
convert gas to stars is independent of the mass of the galaxy).
~ - 2)
as the mass function predicted
[49]
from Press-Schechter theory (i.e. if Press-Schechter theory is valid in this
context, then over this magnitude
range, the combined efficiency of all the baryonic processes which
convert gas to stars is independent of the mass of the galaxy).
An important caveat is that the LFs presented in Figures 2 and 3 are only valid for the cores of rich clusters, which are dense elliptical-rich environments. Perhaps the agreement between the composite LF and the Fornax LF outlined above suggests that it is the elliptical galaxy fraction, not the total galaxy density, that is important (Fornax is anomalously elliptical-rich). There is good evidence [8] that the ellipticals evolve differently from all other giant galaxies (including S0s) in clusters, so it is perhaps unexpected if the global form of the LF is the same in elliptical-rich and elliptical-poor environments.