In the next two sections I will to address two questions. One concerns the interior properties of BCM's and the second concerns the origin of cD halos. The first question comes down to the problem of whether BCM's are a simple extension of the elliptical sequence, in terms of luminosity and structural properties, or whether they are special objects whose formation or evolution is due to some external factor, such as mergers or accretions. At first glance, the naive answer to this question is that BCM's have many properties in common with normal ellipticals. The profiles of D galaxies and the interiors of cD galaxies are basically r1/4 in shape and there is no discontinuity in luminosity from gE and D type galaxies. The diffuse appearance of BCM's, as compared to gE's, is a difficult attribute to quantify. On the other hand, BCM's exhibit luminosity characteristics that imply a two population interpretation (Schneider, Gunn and Hoessel 1983, Bhavsar 1989) as well as external differences from other galaxies, such as their location on density enhancements beyond a mere morphology-density relationship (Beers and Geller 1983).
A crude technique, but still enlightening, is a test of three structural
properties mass (aperture luminosity), scale length (characteristic
radius) and density (surface brightness), three of the four segments
of the fundamental plane. These three diagrams are reproduced in
Figures 4, 5 and 6 from the work of
Schombert (1987).
Figure 4 displays a
plot of aperture magnitude (M16 kpc) versus a
characteristic scale length, in this case the half-light radius,
re, from r1/4
fits. Although BCM's appear to follow a different relationship from
normal ellipticals, closer inspection of this diagram shows that the
bright field ellipticals also deviate from the L
r1.6
line above MV = -21.5. I interpret this to mean that
the kinematic properties of bright ellipticals (rotators below
MV = -21.5 and
velocity supported above) are reflected in the structural relationship
of mass and scale length. In Figure 5, mass
versus density is represented
by magnitude and an inner metric surface brightness (µ at the
2 kpc radius). Similarly in this diagram, BCM's are not strongly deviant,
although the majority appear overly bright for their inner luminosity
densities. On the other hand, the special nature of BCM's can clearly
be seen in a plot of density (effective surface brightness,
µe)
versus scale length (re again) in
Figure 6. Here 87% of the
BCM's lie above the normal sequence, where even the brightest gE galaxies
follow the relationship established by
Kormendy (1980).
I consider
this diagram to be the strongest evidence for structural difference
between BCM's and normal ellipticals. And, I interpret this difference
to be that BCM's are enlarged (have larger effective radii) for a
given surface brightness (rather than higher luminosity density for
a given radii) which is also consistent with a "diffuse"
appearance from morphology. Thus, D and cD galaxies are not in the
same sequence as the elliptical template profiles from
Schombert (1987),
although they are very similar with BCM's being slightly shallower
in profile slope than gE of the same scale length or magnitude. Lastly,
a recent analysis of the fourth leg of the fundamental plane (velocity
dispersion for BCM's and field ellipticals
(Djorgovski et
al. 1990),
from Malumuth and
Kirshner (1985)
data, confirms the above conclusions
finding that BCM's follow different scaling relations.
 |
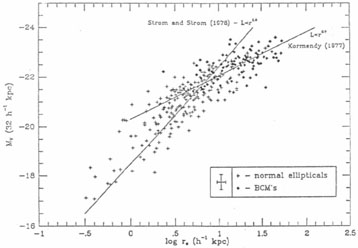Figure 4. Aperture magnitude versus effective radius for normal ellipticals and BCM's. The two lines are relationships taken from early work on ellipticals. |
I have argued in previous papers that these differences on the fundamental plane are exactly what is predicted from N-body merger and accretion simulations. I am particularly influenced by the series of papers by Farouki et al. (1983) for equal mass mergers and hierarchical accretions in which they publish surface density profiles for their remnant objects after each stage of mergers. Sifting through these models and others in the literature (Villumsen 1982, White 1982, May and van Albada 1984) has led me to propose the following scenario for BCM formation and evolution. At the time of galaxy formation there were a range of protogalactic lumps from dwarf sized to 1 or 2 L* sized bodies formed by a dissipative collapse processes (see Larson 1990 for a review of these galaxy building processes). Immediately after this early epoch, all objects which will become bright ellipticals (either field or cluster members) are formed as the product of hierarchical mergers between these early lumps (White and Rees 1978, Tinsley and Larson 1979).
 |
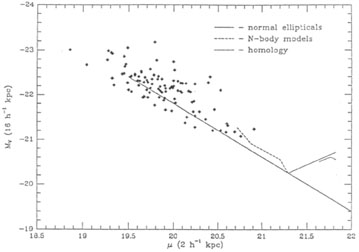Figure 5. Aperture magnitude versus surface brightness for BCM's. BCM's tend to scatter above the relationship for normal ellipticals. |
One argument for this particular origin to all bright ellipticals is shown in Figure 4 where the transition from exponential to r1/4 shaped profiles occurs at the same point where there is a break in the M16 kpc vs re diagram, Figure 4. May and van Albada (1984) argue that a r1/4 profile is a natural result from merging and the simulations of Farouki et al. also note the tendency for an r1/4 profile to form in the remnant. However, to maintain the mass-metallicity relation and the old stellar population observed today, this merging must be at or before the epoch of first star formation. After this early merger epoch, the field and cluster population diverge as the cluster ellipticals continue the process of cannibalizing their neighbors. The field ellipticals, on the other hand, have no neighbors from which to continue this process and, thus, promotes the expectation that cluster ellipticals will depart from the field population only in the degree of dynamical evolution. At this stage, seed cluster ellipticals (ones which will become the BCM's) are located in small subclusters which will later coalesce to form a rich cluster. Within this subgroup, the relative velocities are low and dynamical friction speeds the accretion process. However, unlike hierarchical mergers which led to equalpartition of internal energy and loss of identity of the two original components, later accreting objects will, in all probability, be smaller in mass. Their fate is such that, as they fall into the BCM their outer envelopes are disrupted, placing their stellar material in orbit near the effective radii of BCM's. The remaining small, tightly bound core survives to reach the center of the BCM and increase its central surface brightness (White 1982).
 |
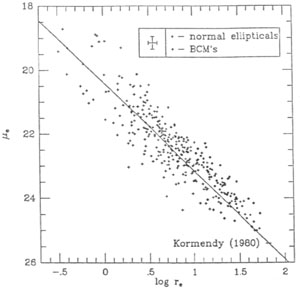Figure 6. Surface brightness versus effective radius for normal ellipticals and BCM's. Most BCM's lie to the right of the normal elliptical relationship as defined by Kormendy (1980). |
After a crossing time (the orbital period at the effective radius), the cannibalized material redistributes into a smooth core and halo r1/4 appearance. The result is that the BCM grows mostly in size due to the fact that the accreting material is located in the outer regions (diffuseness). There is little change in the core surface brightness, relate to other bright ellipticals of the same size or aperture magnitude, while a r1/4 shape is maintained. An interesting special case is if the victim galaxy is not centrally concentrated (e.g. a disk galaxy). In this scenario, the BCM consumes the object yet no core exists to increase the central density of the BCM. The result is a low central surface brightness BCM with dissipating gas collecting in the core, which would be visible as emission gas, if heated by infall, or compressed to ignite star formation. These are precisely the characteristics exhibited by A85 and NGC 6166, our two best examples of low central surface brightness cD's.