

Galaxies occupy a special place in our quest for understanding the Universe. They are large islands in a nearly empty space and contain most of the ordinary baryonic matter, stars and interstellar gas, that emits radiation and can thus be detected by astronomers 1. Galaxies come essentially in two broad categories 2, those in which the luminous mass is arranged in a rotating disk of stars and gas, called disk galaxies or spiral galaxies because of the presence of spiral arms of gas and stars (Figure 1), and those in which the luminous mass is distributed in a smooth, featureless spheroidal structure with little or no rotation, also known as elliptical galaxies (Figure 1). Disk galaxies have a radial light distribution I(r) that is well fit by a decaying exponential law 3, I(r) ~ exp(-r / rd), where rd is a characteristic scale length (rd ~ 2-4 kpc for typical spiral galaxies). Indeed many disk galaxies contain also a spheroidal stellar component at their center, the stellar bulge, which has structural properties similar to an elliptical galaxies albeit being much smaller in size 2. Both types of galaxies are known to contain dark matter, namely matter that is not traced by radiation. In disk galaxies dark matter clearly dominates over luminous matter by mass, as inferred from their high rotation speeds which requires the gravitational pull of a massive and extended halo of dark matter 4. We live in a galaxy of the first kind, the Milky Way. Indeed disk galaxies are ubiquitous in the local Universe, and also at the largest distances and earliest epochs at which the best ground and space-based telescopes have been able to study the morphology of galaxies reliably 5. Only the most massive galaxies in the Universe do not posess a disk component, while this becomes progressively more dominant compared to the spheroidal component as the mass of the galaxy decreases (Figure 2).
 |
 |
Figure 1. Top: a typical disk-dominated galaxy, the nearby spiral galaxy M102 in the Ursa Major constellation, 27 million light years from the Sun (the image was obtained by Chris & Dawn Schur from Payson, Arizona at 5150 feet elevation with an amateur telescope). A small spheroidal bulge is visible at the center of the disk. Bottom: a typical spheroidal galaxy with no disk component, the elliptcal galaxy M87, located at 60 million light years from us (credits in the picture). |
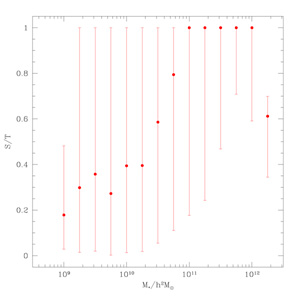 |
Figure 2. The ratio between the mass of the stellar spheroid (S) and the sum of the mass of the stellar spheroid and the stellar disk (T) as a function of galaxy mass from a galaxy sample of the Sloan Digital Sky Surveys (SDSS) 1 2 (2007 Blackwell Publishing Ltd). Red points with error bars show the median S / T as a function of stellar mass together with the 10 and 90 percentiles of the distribution. |
1.1. The theoretical framework
The formation of disk galaxies is one of the major unsolved problems of
modern astrophysics. The basic theoretical framework states that disk
galaxies arise from the gravitational collapse of a rotating
protogalactic cloud of gas within the gravitational potential well of
the dark halo
6.
The gas cools via radiative processes during the collapse and eventually
settles in centrifugal equilibrium at the center of the halo potential
well forming a rotationally supported gas disk
provided that some angular momentum is retained during the collapse
7.
These ideas were
developed two decades ago and they still constitute the backbone
of disk galaxy formation models
8,
9,
10,
11,
12,
13.
What has changed dramatically
since then is the cosmological context in which such idea is applied,
which reflects the remarkable progress that cosmology has undergone in
the meantime. After two decades of active debate there is now one
cosmological paradigm according to which the energy density of the
Universe is dominated by cold dark matter and a cosmological constant,
while ordinary baryonic matter contributes only to a few percent level
(an even smaller contribution is yielded by neutrinos)
14.
This model is supported by observations of the large scale mass
distribution in the Universe traced by galaxies themselves
15
and by the power spectrum of density fluctuations inferred from the cosmic
microwave background radiation
14.
Cold dark matter interacts only via gravity with itself and with ordinary
baryonic matter, and is not subject to any dissipative force.
The governing evolutionary equation for dark matter is the collisionless
Boltzmann equation that describes a zero-pressure fluid, also termed a
collisionless fluid
2.
In this model, called
 CDM (CDM stands
for "cold dark matter", while
CDM (CDM stands
for "cold dark matter", while
 is the
cosmological constant required to explain the observed acceleration of
the Universe) structure forms hierarchically in a bottom-up fashion,
starting from the amplification via gravitational instability of
primordial small density fluctuations in the dark matter
16,
17.
Because of the scale-free nature
of gravity and the dissipationless nature of cold dark matter, in such a
model one expects the formation of self-similar, ellipsoidal collapsed
objects, dark matter halos, at all scales
18.
The largest halos are the last to form
17.
Also, direct three-dimensional simulations of structure formation in a
CDM Universe predict that halos of any mass and size should contain a
swarm of smaller halos, the so-called substructure
19,
20,
as shown in Figure 3.
is the
cosmological constant required to explain the observed acceleration of
the Universe) structure forms hierarchically in a bottom-up fashion,
starting from the amplification via gravitational instability of
primordial small density fluctuations in the dark matter
16,
17.
Because of the scale-free nature
of gravity and the dissipationless nature of cold dark matter, in such a
model one expects the formation of self-similar, ellipsoidal collapsed
objects, dark matter halos, at all scales
18.
The largest halos are the last to form
17.
Also, direct three-dimensional simulations of structure formation in a
CDM Universe predict that halos of any mass and size should contain a
swarm of smaller halos, the so-called substructure
19,
20,
as shown in Figure 3.
 |
Figure 3. Example of a massive dark halo (~
1014 solar masses) assembled by hierarchical merging in a
numerical simulation of the
|
The model predicts quantitatively the size and mass of the dark halo of
a galaxy with a given measured
rotational velocity (the rotational velocity of stars and gas probes the
depth of the galaxy gravitational potential well).
For a galaxy like our own Milky Way, for example, its observed
rotational velocity of ~ 220 km/s implies
a halo mass of about 1012 solar masses and a halo radius of
about 300 kpc
21
(by comparison, the disk of our galaxy contains about 6 ×
1010 solar masses of stars and about 1010 solar
masses of gas
2).
Numerical simulations of the growth of dark matter halos also predict
that the radial density profiles of
such halos diverge near the center and are well described by a
power-law,  ~ r-
~ r- (
( being
the density and r the spherically averaged radius of the halo),
with
being
the density and r the spherically averaged radius of the halo),
with  =
1-1.5
22,
23,
24,
25.
Since dark matter dominates by mass over
ordinary baryonic matter, gas collapses within such halos, eventually
forming a galaxy, because it is pulled inward by their gravitational
attraction rather than collapsing due to its own gravity.
In this scenario there is no such a thing as a galaxy forming in isolation,
rather structure, both dark and baryonic, builds up via continous
accretion and merging of smaller systems
containing a mixture of dark and baryonic matter
26.
This highly dynamical picture emerging from the current cosmology is the
main difference compared to earlier attempts to study galaxy formation.
Halos gain their angular momentum by tidal torques due to asymmetries in
the distribution of matter, and also by acquiring the angular momentum
originally stored in their relative orbit as they come together and
merge into a larger system
27,
28,
29.
Prevailing models have then assumed that baryons and dark matter start
with the same specific angular momentum before the collapse begins since
they are subject to the same tidal torques
8.
=
1-1.5
22,
23,
24,
25.
Since dark matter dominates by mass over
ordinary baryonic matter, gas collapses within such halos, eventually
forming a galaxy, because it is pulled inward by their gravitational
attraction rather than collapsing due to its own gravity.
In this scenario there is no such a thing as a galaxy forming in isolation,
rather structure, both dark and baryonic, builds up via continous
accretion and merging of smaller systems
containing a mixture of dark and baryonic matter
26.
This highly dynamical picture emerging from the current cosmology is the
main difference compared to earlier attempts to study galaxy formation.
Halos gain their angular momentum by tidal torques due to asymmetries in
the distribution of matter, and also by acquiring the angular momentum
originally stored in their relative orbit as they come together and
merge into a larger system
27,
28,
29.
Prevailing models have then assumed that baryons and dark matter start
with the same specific angular momentum before the collapse begins since
they are subject to the same tidal torques
8.
1.2. Computer simulations:the angular momentum problem
The modern tool used to study the hierarchical growth of structure driven by gravity and the concurrent collapse of baryons within dark halos is represented by three-dimensional computer simulations that solve the gravitational and hydrodynamical forces between parcels of gas and dark matter. We will discuss the methodology employed by such simulations in the next section. For now it suffices to say that in the most popular simulation method both the gas (i.e. the baryonic component) and the dark matter are represented by particles so that structures are discretized in mass and space. The evolutionary equations, such as the collisionless Boltzmann equation for cold dark matter, the Euler equation for baryonic matter (baryonic matter is treated as an ideal gas) and the Poisson equation, which holds for both, are solved for such discrete representation of physical reality. Available methods to discretize physical variables and governing equations are constructed in such a way that they should converge to the exact continuum solution for an infinite number of particles. As we will see in the next section, discretization itself, along with other aspects of the current methods, can introduce spurious effects in the computer models. Simulations take advantage of large parallel supercomputers in which hundreds of processing units are used simultaneously to compute the forces and advance the system to the next timestep.
One important prediction of simulations of a CDM Universe
is that halos have a rather universal value of the angular momentum (per
unit mass) at any given epoch quite irrespective of their precise mass
assembly history. This is parameterized via the dimensionless spin
parameter  = J
E1/2 / GM5/2, where E,
M and J are the total energy, mass and angular momentum of
the dark halo (G is the gravitational constant).
One can show that
= J
E1/2 / GM5/2, where E,
M and J are the total energy, mass and angular momentum of
the dark halo (G is the gravitational constant).
One can show that  is
proportional to the ratio between the rotational kinetic energy and
the kinetic energy in disordered motions associated with the halo.
Halos have a universal distribution of spin parameters, which peaks at a
value
is
proportional to the ratio between the rotational kinetic energy and
the kinetic energy in disordered motions associated with the halo.
Halos have a universal distribution of spin parameters, which peaks at a
value  ~ 0.035
29.
~ 0.035
29.
Simple spherical one-dimensional models that study disk formation in an isolated CDM halo (namely a halo that does not interact or merge with other halos) predict that the size of disks resulting from the infall and collapse of baryons matches the size of observed disks in galaxies very well 8. The models use mainly two inputs, both coming from cosmological simulations, the halo density profile, which is related to the gravitational pull that drives the gas collapse, and the initial specific angular momentum of gas as implied by the typical values of the spin parameter. They further assume that angular momentum is conserved during the collapse. Hence this result is simple and remarkable at the same time; it says that CDM halos have the right amount of angular momentum to form observed disk galaxies.
For more than a decade researchers have tried to reproduce the latter result with fully three-dimensional computer simulations but have run into several problems. It was soon realized that, once the hypothesis of isolation is removed and hierarchical merging is accounted for, angular momentum can be lost by the gas to the dark matter due to a process known as dynamical friction 30, 2, 31. During mergers, previously collapsed clumps of gas and dark matter fall into a larger dark halo and suffer a drag force as they move through the latter. The loss of angular momentum caused by the drag force, called "dynamical friction", is more effective when the gas is distributed into cold and dense lumps rather than being smooth and extended 32. But gas is expected to be clumpy in a model with collisionless cold dark matter in which collapse can occur at all scales, and large halos grow by accreting smaller halos which bring their own dense collapsed gas. As a result, early simulations 32 were obtaining improbable small disks with ten times less angular momentum than real ones. Two types of solutions for this "angular momentum problem" have been considered since then. The first is very drastic and calls for revising the cosmological model itself. Alternative models in which the dark matter has a non-negligible thermal velocity rather then being "cold" would produce collapsed systems only above a characteristic scale because the thermal jittering will tend to smear out short-wavelength density perturbations 33. These warm dark matter models (WDM) behave like CDM on large scale, thus maintaining its succesful features. The reduced clumpiness of dark matter halos in the WDM model implies that baryons are smoothly distributed rather than arranged in previously collapsed dense lumps when they fall into large galaxy-sized halos, and therefore lose less angular momentum by dynamical friction 33, 34. The second, less exotic possibility, is that baryons do not just follow the merging hierarchy imposed by dark matter but somehow decouple from it and remain much smoother. This could happen if the thermal energy content of baryons was enough to resist gravitational collapse, at least up to some critical mass scale. This way a fraction of the gas that would have entered a halo in dense clumps within smaller halos would instead enter with a smooth distribution, perhaps avoiding catastrophic loss of angular momentum. Various plausible astrophysical mechanisms can be responsible for increasing the thermal energy content of the baryons, for example the energy injection by supernovae explosions and the ambient radiation field produced by stars, accreting black holes or also external galaxies. There is, however, a third possibility. This is that the baryons clump excessively in computer simulations because the numerical methods adopted can introduce artificial loss of angular momentum. As we argue in this report, a solution lies probably in a combination of the latter two proposals, with no need of revising the standard cosmological structure formation model.
The next two sections will be devoted, respectively, to the role of numerical effects in disk formation simulations, and to the modeling of gas thermodynamics and star formation in the simulations. We will then show how the structure of simulated disks is affected by different models of thermodynamics and star formation. Finally, we will summarize the current status of the field and the major problems that remain to be solved, including the puzzling origin of disk galaxies without a bulge. We will attempt to recall the most important contributions by the various groups actively involved in this field of research while at the same time covering in more detail some recent results of the research group to which the authors of this report belong.