


2.1. WHIM ionisation conditions
The occurrence and characteristics of the WHIM absorption signatures in the FUV and X-ray band are determined to a high degree by the ionisation conditions in the gas. We briefly discuss the WHIM ionisation properties, as this is crucial for interpretation of the WHIM absorption lines in FUV and X-ray spectra that arise in such warm-hot gas. Generally, there are two processes that determine the ionisation state of warm-hot gas in the intergalactic medium: collisional ionisation caused by the high temperature of the gas in collapsed structures and photoionisation by the cosmic FUV background.
By far most of the mass of the WHIM is in the form of ionised hydrogen. Therefore, understanding the processes that lead to the ionisation of hydrogen is essential for the interpretation of WHIM absorption lines and for a reliable estimate of the baryon content of warm-hot intergalactic gas. The ionisation potential of neutral hydrogen is 13.6 eV and thus both ionisation by particle collisions and ionisation by high-energy photons contribute to the ionisation of H I in warm-hot gas. We start with collisional ionisation, which is believed to dominate the ionisation of hydrogen at temperatures > 105 K.
In collisional ionisation equilibrium (CIE) - the most
simple approach to characterise the ionisation conditions
in low-density, high-temperature plasmas - the ionisation fraction
depends only on the gas temperature. If we ignore any charge-exchange
reactions (which is justified in case of hydrogen), the neutral hydrogen
fraction in CIE is simply the ratio between the recombination coefficient
 H(T)
and the collisional ionisation coefficient
H(T)
and the collisional ionisation coefficient
 H(T):
H(T):
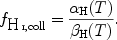 |
(1) |
Above gas temperatures of ~ 1.5 × 104 K collisions by thermal electrons efficiently ionise hydrogen to a high degree, and already at T ~ 3 × 104 K the neutral hydrogen fraction in the gas is less then one percent. For the temperature range that is characteristic for the WHIM, T = 105 - 107 K, one can approximate the ionisation fraction in a collisional ionisation equilibrium in the way
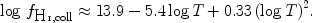 |
(2) |
where T is in units K (Richter et al. 2006a; Sutherland & Dopita 1993). Thus, for WHIM gas with T = 106 K the neutral hydrogen fraction in the gas in CIE is only ~ 2.4 × 10-7.
Next to particle collisions, photons with energies > 13.6 eV contribute to the ionisation of the WHIM, in particular in the low-temperature WHIM tail at ~ 105 K and below. Such ionising photons in intergalactic space are indeed provided by the metagalactic ultraviolet (UV) background, originating from the hard radiation emitted by QSOs and AGN. Fig. 1 shows the spectral shape of the UV background at z = 0 (left panel) and the redshift-dependence of the hydrogen photoionisation rate from the UV background (right panel) based on the models by Haardt & Madau (1996).
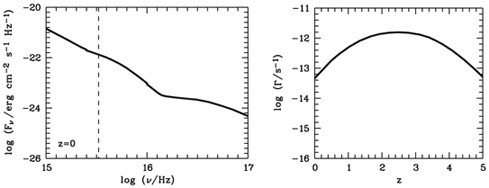 |
Figure 1. Left panel: Spectral shape
of the metagalactic UV background at z = 0 (from
Haardt &
Madau 1996).
Plotted is the flux of photons
(F |
Considering photoionisation, one generally can write for the neutral-hydrogen fraction in the gas:
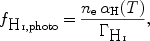 |
(3) |
where
 H(T)
denotes the temperature-dependent recombination rate of hydrogen,
ne is the electron density, and
H(T)
denotes the temperature-dependent recombination rate of hydrogen,
ne is the electron density, and
 H I
is the photoionisation rate.
H I
is the photoionisation rate.
 H I
depends on the ambient ionising radiation field
J
H I
depends on the ambient ionising radiation field
J (in units erg cm-2 s-1 Hz-1
sr-1) in the WHIM provided by the metagalactic UV background
(see Fig. 1):
(in units erg cm-2 s-1 Hz-1
sr-1) in the WHIM provided by the metagalactic UV background
(see Fig. 1):
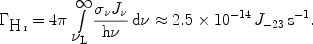 |
(4) |
Here,  L is
the frequency at the Lyman limit
and
L is
the frequency at the Lyman limit
and 
 denotes the
photoionisation cross section of hydrogen, which scales with
denotes the
photoionisation cross section of hydrogen, which scales with
 -3 for frequencies
larger that
-3 for frequencies
larger that  L (see
Kaastra et
al. 2008
- Chapter 9, this volume).
We have introduced the dimensionless scaling factor
J-23 which gives the metagalactic UV radiation
intensity at the Lyman limit in units
10-23 erg cm-2 s-1 Hz-1
sr-1. For z = 0 we have J-23 ~ 1-2,
while for z = 3 the value for J-23 is ~ 80,
thus significantly higher
(Haardt &
Madau 1996).
Assuming ne = nH and inserting a
proper function for
L (see
Kaastra et
al. 2008
- Chapter 9, this volume).
We have introduced the dimensionless scaling factor
J-23 which gives the metagalactic UV radiation
intensity at the Lyman limit in units
10-23 erg cm-2 s-1 Hz-1
sr-1. For z = 0 we have J-23 ~ 1-2,
while for z = 3 the value for J-23 is ~ 80,
thus significantly higher
(Haardt &
Madau 1996).
Assuming ne = nH and inserting a
proper function for
 H(T),
we finally can write for the logarithmic neutral hydrogen fraction in a
purely photoionised WHIM plasma
H(T),
we finally can write for the logarithmic neutral hydrogen fraction in a
purely photoionised WHIM plasma
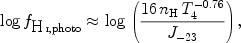 |
(5) |
where nH is the hydrogen volume density
in units cm-3 and T4 is the temperature in
units 104 K. Thus, for purely photoionised intergalactic
gas at z = 0 with n = 5 × 10-6 and
T = 106 K we find that the neutral hydrogen fraction
is fH I, photo ~ 2.4 × 10-6.
This is ten times higher than for CIE,
indicating that collisions dominate the ionisation fraction
of hydrogen in intermediate and high-temperature WHIM regions.
However, note that at lower temperatures near T = 105 K
at the same density we have fH I, photo
~ fH I, coll. Since this is the WHIM temperature
regime preferentially detected by UV absorption features
(e.g., O VI and broad
Ly ), photoionisation
is important and needs to be accounted for when it comes to
the interpretation of WHIM absorbers observed in the FUV.
From a WHIM simulation at z = 0
including both collisional ionisation and photoionisation
(Richter et
al. 2006b;
see Fig. 2)
find the following empirical relation between neutral hydrogen
fraction and gas temperature for a WHIM
density range between log nH = -5.3 and -5.6:
), photoionisation
is important and needs to be accounted for when it comes to
the interpretation of WHIM absorbers observed in the FUV.
From a WHIM simulation at z = 0
including both collisional ionisation and photoionisation
(Richter et
al. 2006b;
see Fig. 2)
find the following empirical relation between neutral hydrogen
fraction and gas temperature for a WHIM
density range between log nH = -5.3 and -5.6:
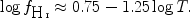 |
(6) |
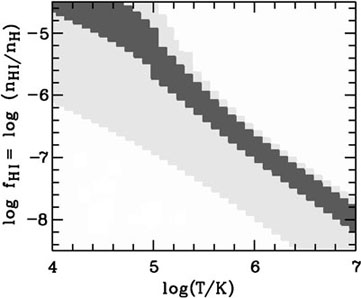 |
Figure 2. The neutral hydrogen fraction, log fH I = log (nH I / nH), in a WHIM simulation (photoionisation+collisional ionisation), is plotted as a function of the gas temperature, log T. The light gray shaded indicates cells in the density range log nH = -5 to -7. The dark gray shaded area refers to cells that have log nH = -5.3 to -5.6, thus a density range that is characteristic for WHIM absorbers. Adapted from Richter et al. (2006b). |
This equation may serve as a thumb rule to estimate ionisation fractions in WHIM absorbers at z = 0 if the gas temperature is known (e.g., from measurements of the line widths; see Sect. 2.2.1).
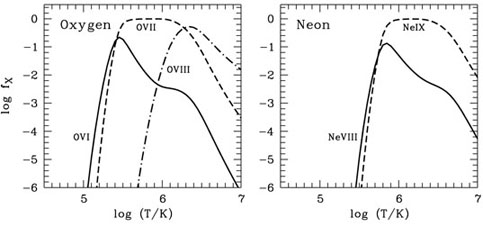 |
Figure 3. CIE ion fractions of selected high ions of oxygen (O VI, O VII, O VIII; left panel) and neon (Ne VIII, Ne IX; right panel) in the WHIM temperature range log (T/K) = 4.5 - 7.0, based on calculations by Sutherland & Dopita (1993). |
While hydrogen provides most of the mass in the WHIM, the most important diagnostic lines to study this gas phase are from highly ionised metals such as oxygen, neon, carbon, magnesium, and others. Therefore, the understanding of the ionisation properties of the observed high ions of these elements is as important as for hydrogen. As for hydrogen, both collisional ionisation and photoionisation need to be considered. With its single electron, hydrogen can only be either neutral or fully ionised. Heavy elements, in contrast, have several electrons available and are - even at very high temperatures - usually only partly ionised. Thus, electronic transitions exist for such highly-ionised metals ("high ions") in warm-hot gas. Of particular importance for observations of the WHIM are the high ionisation states of oxygen, O VI, O VII, and O VIII, as they have strong electronic transitions in the UV (O VI) and at X-ray wavelengths (O VII & O VIII) and oxygen is a relatively abundant element. Another important metal for observing warm-hot gas in the UV and X-ray band is neon (Ne VII, Ne VIII, Ne IX, Ne X). In collisional ionisation equilibrium, the ionisation state of these elements is determined solely by the temperature of the gas. For each element, the ionisation fractions of the ionisation states (e.g., four-times vs. five-times ionised) then are characterised by the respective ionisation potentials (IPs) of the individual ionisation levels. For instance, at T ~ 1-3 × 105 K, a significant fraction of the oxygen is five-times ionised (O+5 or O VI, IP = 138 eV). Six-times ionised oxygen (O+6 or O VII, IP = 739 eV) and seven-times ionised oxygen (O+7 or O VIII, IP = 871 eV) predominantly exist at higher temperatures in the range 3 × 105 - 3 × 106 K and 3 × 106 - 107 K, respectively. Fig. 3 shows the ionisation fractions of the most important high ions of oxygen and neon, based on the CIE calculations of Sutherland & Dopita (1993); see also Kaastra et al. 2008 - Chapter 9, this volume. High ions of other elements such as carbon, nitrogen, silicon and magnesium are less important for WHIM observations as their observable transitions trace lower temperature gas (e.g., C IV, Si IV) or the abundance of these elements in the intergalactic medium are too low. It is important to note at this point, that the discussed relation between ionisation state/fraction and gas temperature explicitly assumes that the gas is in an ionisation equilibrium. This may not be generally the case in the WHIM, however, as the densities are generally very low. For instance, under particular non-equilibrium conditions the timescales for cooling, recombination, and ion/electron equilibration may differ significantly from each other (see for instance Bykov et al. 2008 - Chapter 8, this volume). In such a case, the presence of high ions such as O VI and/or measured high-ion ratios would not serve as a reliable "thermometer" for the WHIM gas. In addition, WHIM filaments most likely neither are isothermal nor do they have a constant particle density. In fact, as WHIM simulations demonstrate, WHIM absorbers seem to represent a mix of cooler photoionised and hotter collisionally ionised gas with a substantial intrinsic density range. The absorption features from high ions arising in such a multi-phase medium therefore are generally difficult to interpret in terms of physical conditions and baryon budget.
In view of the high energies required to produce the high ions of oxygen and neon in combination with the spectral shape of the metagalactic background radiation (see Fig. 1), photoionisation of high metal ions in the WHIM is less important than for hydrogen. However, for O VI photoionisation is important at low redshifts in WHIM regions with very low densities or in systems located close to a strong local radiation source (e.g., in O VI systems associated with the background QSO). Note that at high redshift, most of the intervening O VI appears to be photoionised owing to the significantly higher intensity of the metagalactic background radiation in the early Universe (see Sect. 5.2).
2.2. WHIM absorption signatures in the UV and X-ray band
As indicated in the previous subsection, five-times ionised oxygen (O VI) is
by far the most important high ion to trace the WHIM at temperatures of
T ~ 3 × 105 K in the ultraviolet regime
(assuming CIE, see above).
Oxygen is a relatively abundant element and the
two lithium-like (1s22s)2
S1/2
 (1s22p)2P1/2,3/2
electronic transitions of O VI located in the FUV at 1031.9 and 1037.6
Å have large oscillator strengths (f1031 =
0.133, f1037 = 0.066). Next to O VI,
Ne VIII traces WHIM gas near T ~ 7 ×105 K (in
collisional ionisation equilibrium) and thus
is possibly suited to complement the O VI measurements
of the WHIM in a higher temperature regime.
The two available Ne VIII lines are located in the extreme
ultraviolet (EUV) at 770.4 Å (f770 = 0.103) and
780.3 Å (f780 = 0.051), allowing us to trace
high-column density WHIM absorbers at redshifts z > 0.18
with current FUV satellites such as FUSE.
However, as the cosmic abundance of Ne VIII is relatively low,
Ne VIII is not expected to be a particularly sensitive tracer of the
WHIM at the S/N levels achievable with current UV
spectrographs. The same argument holds for the high ion Mg X,
which has two transitions in the EUV at even lower wavelengths
(
(1s22p)2P1/2,3/2
electronic transitions of O VI located in the FUV at 1031.9 and 1037.6
Å have large oscillator strengths (f1031 =
0.133, f1037 = 0.066). Next to O VI,
Ne VIII traces WHIM gas near T ~ 7 ×105 K (in
collisional ionisation equilibrium) and thus
is possibly suited to complement the O VI measurements
of the WHIM in a higher temperature regime.
The two available Ne VIII lines are located in the extreme
ultraviolet (EUV) at 770.4 Å (f770 = 0.103) and
780.3 Å (f780 = 0.051), allowing us to trace
high-column density WHIM absorbers at redshifts z > 0.18
with current FUV satellites such as FUSE.
However, as the cosmic abundance of Ne VIII is relatively low,
Ne VIII is not expected to be a particularly sensitive tracer of the
WHIM at the S/N levels achievable with current UV
spectrographs. The same argument holds for the high ion Mg X,
which has two transitions in the EUV at even lower wavelengths
(
 609.8, 624.9 Å). So
far, only O VI and in one case Ne VIII has been observed in the WHIM
at low redshift (see Sect. 3.2). Note
that WHIM absorption features by O VI (and Ne VIII) are mostly unsaturated
and the line profiles are fully or nearly resolved by current
UV instruments such as FUSE and STIS, which provide spectral
resolutions of R =
609.8, 624.9 Å). So
far, only O VI and in one case Ne VIII has been observed in the WHIM
at low redshift (see Sect. 3.2). Note
that WHIM absorption features by O VI (and Ne VIII) are mostly unsaturated
and the line profiles are fully or nearly resolved by current
UV instruments such as FUSE and STIS, which provide spectral
resolutions of R =
 /
/ 

 20,000 and 45,000,
respectively. Table 1 summarises physical
parameters of O and Ne high ions and their observable transitions in the
UV and X-ray bands.
20,000 and 45,000,
respectively. Table 1 summarises physical
parameters of O and Ne high ions and their observable transitions in the
UV and X-ray bands.
| Ion | [X/H]1 | Ionisation | Absorption | Band | CIE temperature2 |
| potential [eV] | lines [Å] | range [106 K] | |||
| O VI | -3.34 | 138 | 1031.926 | FUV | 0.2-0.5 |
| 1037.617 | |||||
| O VII | -3.34 | 739 | 21.602 | X-ray | 0.3-3.0 |
| O VIII | -3.34 | 871 | 18.969 | X-ray | 1.0-10.0 |
| Ne VIII | -4.16 | 239 | 770.409 | EUV | 0.5-1.3 |
| 780.324 | |||||
| Ne IX | -4.16 | 1196 | 13.447 | X-ray | 0.6-6.3 |
1 [X/H] is the log of the number density of element X
relative to hydrogen for Solar abundances, taken here from
Asplund et
al. (2004). |
|||||
Four-times ionised nitrogen (N V; I.P. is 98 eV) also
is believed to trace predominantly collisionally ionised gas at temperatures
near T ~ 2 × 105 K, but its lower cosmic
abundance together with its deficiency in low metallicity environments
due to nucleosynthesis effects (e.g.,
Pettini et
al. 2002)
makes it very difficult to detect in the WHIM.
Other available strong high-ion transitions in the UV
from carbon (C IV 
 1548.2, 1550.8 Å) and
silicon (Si IV
1548.2, 1550.8 Å) and
silicon (Si IV 
 1393.8, 1402.8 Å) are
believed to trace mainly photoionised gas at temperatures T <
105 K, but not the shock-heated warm-hot gas at higher
temperatures.
1393.8, 1402.8 Å) are
believed to trace mainly photoionised gas at temperatures T <
105 K, but not the shock-heated warm-hot gas at higher
temperatures.
Next to high-ion absorption from heavy elements, recent UV observations
(Richter et
al. 2004;
Sembach et
al. 2004;
Lehner et
al. 2007)
have indicated that WHIM filaments
can be detected in Ly absorption of neutral hydrogen.
Although the vast majority of the hydrogen in the WHIM
is ionised (by collisional processes and UV radiation), a
tiny fraction (fH I < 10-5, typically)
of neutral hydrogen is expected to be present. Depending on the total
gas column density of a WHIM absorber and its temperature, weak H I
Ly
absorption of neutral hydrogen.
Although the vast majority of the hydrogen in the WHIM
is ionised (by collisional processes and UV radiation), a
tiny fraction (fH I < 10-5, typically)
of neutral hydrogen is expected to be present. Depending on the total
gas column density of a WHIM absorber and its temperature, weak H I
Ly absorption
at column densities 12.5
absorption
at column densities 12.5  log N(H I)
log N(H I)  14.0
may arise from WHIM filaments and could be used to
trace the ionised hydrogen component.
The Ly
14.0
may arise from WHIM filaments and could be used to
trace the ionised hydrogen component.
The Ly absorption from
WHIM filaments is very broad due to thermal line
broadening, resulting in large Doppler parameters
of b > 40 km s-1. Such lines are generally difficult
to detect, as they are broad and shallow. High resolution,
high S/N FUV spectra of QSOs with smooth background continua
are required to successfully search for broad
Ly
absorption from
WHIM filaments is very broad due to thermal line
broadening, resulting in large Doppler parameters
of b > 40 km s-1. Such lines are generally difficult
to detect, as they are broad and shallow. High resolution,
high S/N FUV spectra of QSOs with smooth background continua
are required to successfully search for broad
Ly absorption in the low-redshift WHIM. STIS installed on the HST
is the only instrument that has provided such data,
but due to the instrumental limitations of space-based
observatories, the number of QSO spectra adequate for searching
for WHIM broad Ly
absorption in the low-redshift WHIM. STIS installed on the HST
is the only instrument that has provided such data,
but due to the instrumental limitations of space-based
observatories, the number of QSO spectra adequate for searching
for WHIM broad Ly absorption (in the following abbreviated as "BLA") is very limited.
absorption (in the following abbreviated as "BLA") is very limited.
The b values of the BLAs are assumed to be composed
of a thermal component, bth, and a non-thermal
component, bnt, in the way that
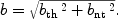 |
(7) |
The non-thermal component may include processes like macroscopic turbulence, unresolved velocity-components, and others (see Richter et al. 2006a for a detailed discussion). The contribution of the thermal component to b depends on the gas temperature:
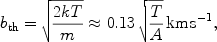 |
(8) |
where T is in K, k is the Boltzmann constant, m is
the particle mass, and A is the atomic weight.
For the shock-heated WHIM gas with log T
 5 one thus expects
bth
5 one thus expects
bth  40
km s-1. The non-thermal broadening mechanisms
are expected to contribute to some degree to the total
b values in WHIM absorbers (see
Richter et
al. 2006a),
so that the measured b value of a BLA provides only an upper
limit for the temperature of the gas.
40
km s-1. The non-thermal broadening mechanisms
are expected to contribute to some degree to the total
b values in WHIM absorbers (see
Richter et
al. 2006a),
so that the measured b value of a BLA provides only an upper
limit for the temperature of the gas.
The highest ionisation phase of the WHIM will produce and absorb line
radiation primarily in the He- and H-like ions of the low-Z elements
(C, N, O, Ne), and possibly in the L-shell ions of Fe. In practice, much
of the attention is focused on oxygen, because of its relatively high
abundance, and because the strongest resonance lines in He- and H-like O
are in a relatively 'clean' wavelength band. For reference, the
Ly transitions of C VI,
N VII, O VIII, and Ne X occur at 33.7360, 24.7810, 18.9689,
and 12.1339 Å, respectively (wavelengths of the 1s -
2p1/2,3/2 doublet weighted with oscillator strength;
Johnson &
Soff (1985).
The He-like ions C V, N VI, O VII, and Ne IX have their strongest
transition, the n = 1-2 resonance line, at 40.2674, 28.7800,
21.6015, and 13.4473 Å
(Drake 1988;
see also Table 1). Data on the higher order
series members can be found in
Verner et
al. (1996).
As far as the Fe L shell ions are concerned, the most likely transition
to show up would be the
strongest line in Ne-like Fe XVII, n = 2p - 3d
transitions of C VI,
N VII, O VIII, and Ne X occur at 33.7360, 24.7810, 18.9689,
and 12.1339 Å, respectively (wavelengths of the 1s -
2p1/2,3/2 doublet weighted with oscillator strength;
Johnson &
Soff (1985).
The He-like ions C V, N VI, O VII, and Ne IX have their strongest
transition, the n = 1-2 resonance line, at 40.2674, 28.7800,
21.6015, and 13.4473 Å
(Drake 1988;
see also Table 1). Data on the higher order
series members can be found in
Verner et
al. (1996).
As far as the Fe L shell ions are concerned, the most likely transition
to show up would be the
strongest line in Ne-like Fe XVII, n = 2p - 3d
 15.014 Å. In
addition, all lower ionisation stages of C, N, O, and Ne (with the
exception of neutral Ne of course)
can also absorb by n = 1-2; the strongest of these transitions
would be 1s - 2p in O VI at 22.019 Å
(Schmidt et
al. 2004).
Likewise, the lower ionisation stages of
Fe could in principle produce n = 2-3 absorption.
15.014 Å. In
addition, all lower ionisation stages of C, N, O, and Ne (with the
exception of neutral Ne of course)
can also absorb by n = 1-2; the strongest of these transitions
would be 1s - 2p in O VI at 22.019 Å
(Schmidt et
al. 2004).
Likewise, the lower ionisation stages of
Fe could in principle produce n = 2-3 absorption.
The thermal widths of all these transitions will be very small, requiring resolving powers of order R ~ 10000 (C, N, O, Ne) for gas temperatures of order 106 K to be resolved; for Fe, the requirement is even higher, by a factor ~ 2. As we will see, for practical reasons, these requirements exceed the current capabilities of astrophysical X-ray spectroscopy by a large factor. Due to the small Doppler broadening (ignoring turbulent velocity fields for now), the lines will rapidly saturate. For He- and H-like O resonance line absorption, saturation sets in at an equivalent width of order 1 mÅ (Kaastra et al. 2008) - Chapter 9, this volume), or column densities of order a few times 1014 ions cm-2. The challenge, therefore, for X-ray spectroscopy presented by the IGM is to detect small equivalent width, near-saturation lines that are unresolved.
2.3. The baryon content of the WHIM as measured by UV and X-ray absorbers
One important result from absorption line measurements of the WHIM in the UV
is the observed number density of WHIM absorbers, usually expressed as
dN / dz, the number of absorbers per unit
redshift. For instance, from
recent measurements with FUSE and HST/STIS one finds for O VI absorbers and
Broad Ly absorbers at
z
absorbers at
z  0 values of
dN / dz(O VI)
0 values of
dN / dz(O VI)
 20 and
dN / dz(BLA)
20 and
dN / dz(BLA)
 30
(see Sect. 3.2).
Currently, the WHIM absorber density is only measurable in the UV,
since in the X-ray band both the observed number of WHIM absorption
lines and the available redshift path for WHIM observations is too small
to derive statistically significant values of dN /
dz(O VII) and dN / dz(O VIII).
30
(see Sect. 3.2).
Currently, the WHIM absorber density is only measurable in the UV,
since in the X-ray band both the observed number of WHIM absorption
lines and the available redshift path for WHIM observations is too small
to derive statistically significant values of dN /
dz(O VII) and dN / dz(O VIII).
A particularly interesting question now is, how the observed number
density of high-ion lines or BLAs translates into an estimate of the
cosmological baryon mass density of the WHIM,
 b(WHIM).
To obtain such an estimate of the baryon content of the WHIM from UV and
X-ray absorption measurements one has to consider two main steps. First,
one needs to transform the observed column densities of the high ions
(e.g., O VI, O VII, O VIII) into a total gas column density by
modelling the ionisation conditions in the gas. In a second step, one then
integrates over the total gas column densities of all observed WHIM
absorbers along the given redshift path and from that derives
b(WHIM).
To obtain such an estimate of the baryon content of the WHIM from UV and
X-ray absorption measurements one has to consider two main steps. First,
one needs to transform the observed column densities of the high ions
(e.g., O VI, O VII, O VIII) into a total gas column density by
modelling the ionisation conditions in the gas. In a second step, one then
integrates over the total gas column densities of all observed WHIM
absorbers along the given redshift path and from that derives
 b(WHIM) for
a chosen cosmology. Throughout the paper we will assume
a
b(WHIM) for
a chosen cosmology. Throughout the paper we will assume
a  CDM cosmology
with H0 = 70 km s-1 Mpc-1,
CDM cosmology
with H0 = 70 km s-1 Mpc-1,

 =
0.7,
=
0.7,  m =
0.3, and
m =
0.3, and  b
= 0.045. For the first step the uncertainty lies in the estimate of
the ionisation fraction of hydrogen of the WHIM. For this, it is
usually assumed that the WHIM is in collisional ionisation
equilibrium, but photoionisation and non-equilibrium conditions
may play a significant role. In the case of using metal ions such as O VI
the unknown oxygen abundance (O/H) of the gas introduces an additional
uncertainty (see below) for the estimate of
b
= 0.045. For the first step the uncertainty lies in the estimate of
the ionisation fraction of hydrogen of the WHIM. For this, it is
usually assumed that the WHIM is in collisional ionisation
equilibrium, but photoionisation and non-equilibrium conditions
may play a significant role. In the case of using metal ions such as O VI
the unknown oxygen abundance (O/H) of the gas introduces an additional
uncertainty (see below) for the estimate of
 b(WHIM).
For the second step, it is important to have a large enough
sample of WHIM absorption lines and a sufficient total redshift path
along different directions in order to handle statistical errors
and the problem of cosmic variance. As mentioned earlier, these
requirements currently are fulfilled only for the UV absorbers.
b(WHIM).
For the second step, it is important to have a large enough
sample of WHIM absorption lines and a sufficient total redshift path
along different directions in order to handle statistical errors
and the problem of cosmic variance. As mentioned earlier, these
requirements currently are fulfilled only for the UV absorbers.
The cosmological mass density
 b of O VI
absorbers (and, similarly, for other high ions)
in terms of the current critical density
b of O VI
absorbers (and, similarly, for other high ions)
in terms of the current critical density
 c can
be estimated by
c can
be estimated by
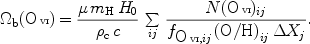 |
(9) |
In this equation, μ=1.3 is the mean molecular weight,
mH = 1.673 × 10-27 kg is the mass per
hydrogen atom, H0 is the adopted local Hubble constant,
and  c = 3H02 /
8
c = 3H02 /
8  G is the current
critical density.
The index i denotes an individual high-ion absorption system
along a line of sight j. Each measured high-ion absorption
system i is characterised
by its measured ion column density (e.g., N(O VI)ij),
the ionisation fraction of the measured ion (e.g.,
fO VI,ij),
and the local abundance of the element measured compared to
hydrogen (e.g., the local oxygen-to-hydrogen ratio, by number).
Each line of sight j has a characteristic redshift range
G is the current
critical density.
The index i denotes an individual high-ion absorption system
along a line of sight j. Each measured high-ion absorption
system i is characterised
by its measured ion column density (e.g., N(O VI)ij),
the ionisation fraction of the measured ion (e.g.,
fO VI,ij),
and the local abundance of the element measured compared to
hydrogen (e.g., the local oxygen-to-hydrogen ratio, by number).
Each line of sight j has a characteristic redshift range
 z
in which high-ion absorption may be detected.
The corresponding comoving path length
z
in which high-ion absorption may be detected.
The corresponding comoving path length
 X
available for the detection of WHIM high-ion absorbers
then is given by:
X
available for the detection of WHIM high-ion absorbers
then is given by:
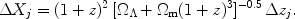 |
(10) |
In analogy, we can write for the cosmological mass density of the BLAs:
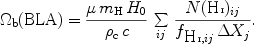 |
(11) |
As can be easily seen, the advantage of using BLAs for deriving the WHIM
mass density is
that the metallicity of the gas is unimportant for the determination
of  b.
The disadvantage is, however, that the ionisation
corrections are very large and uncertain, since they are determined
indirectly from the BLA line widths (see Sect. 2.2.1).
b.
The disadvantage is, however, that the ionisation
corrections are very large and uncertain, since they are determined
indirectly from the BLA line widths (see Sect. 2.2.1).