


A remarkable change in the turbulent dynamo action occurs if the turbulence is helical. This can be clearly seen for example in the simulations by Brandenburg [19], where a large scale field, on the scale of the box develops when a helical forcing is employed, even though the forcing itself is on a scale about 1/5th the size of the box. The large scale field however in these closed box simulations develops only on the long resistive timescales. It is important to understand how such a field develops and how one can generate a large scale field on a faster timescale. The possible importance of helical turbulence for large-scale field generation was proposed by Parker [20], and is in fact discussed in text books [21]. We summarize briefly below the theory of the mean-field dynamo (MFD) as applied to magnetic field generation in disk galaxies, turn to several potential problems that have been recently highlighted and their possible resolution.
Suppose the velocity field is split into
the sum of a mean, large-scale velocity
 and a turbulent, stochastic velocity u.
The induction equation becomes a stochastic
partial differential equation.
Let us split the magnetic field also as B =
and a turbulent, stochastic velocity u.
The induction equation becomes a stochastic
partial differential equation.
Let us split the magnetic field also as B =
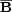 + b,
into a mean field
+ b,
into a mean field
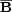 = <B> and a
fluctuating component b. Here the average <>, is defined
either as a spatial average over scales larger than the turbulent
eddy scales (but smaller than the system size) or as an ensemble average.
Taking the average of the induction equation 2.1, one gets
the mean-field dynamo equation for
= <B> and a
fluctuating component b. Here the average <>, is defined
either as a spatial average over scales larger than the turbulent
eddy scales (but smaller than the system size) or as an ensemble average.
Taking the average of the induction equation 2.1, one gets
the mean-field dynamo equation for
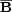 ,
,
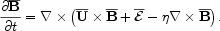 |
(4) |
This averaged equation now has a new term,
the mean electromotive force (emf)
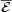 =
=
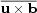 ,
which crucially depends on the statistical properties of
the small-scale velocity and magnetic fields.
A central closure problem in MFD theories is
to compute the mean emf
,
which crucially depends on the statistical properties of
the small-scale velocity and magnetic fields.
A central closure problem in MFD theories is
to compute the mean emf
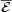 and express it in terms of the mean field itself.
In the two-scale approach one assumes that the mean field is spatially
smooth over scales bigger than the turbulence coherence scale l,
and expresses the mean emf
and express it in terms of the mean field itself.
In the two-scale approach one assumes that the mean field is spatially
smooth over scales bigger than the turbulence coherence scale l,
and expresses the mean emf
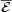 mean magnetic field and its first derivative
[21].
For isotropic, homogeneous, helical 'turbulence'
in the approximation that the correlation time
mean magnetic field and its first derivative
[21].
For isotropic, homogeneous, helical 'turbulence'
in the approximation that the correlation time
 is short (ideally
u
is short (ideally
u / l <<
1, where u is the
typical turbulent velocity) one employs what is known as the
First order smoothing approximation (FOSA) to write
/ l <<
1, where u is the
typical turbulent velocity) one employs what is known as the
First order smoothing approximation (FOSA) to write
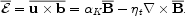 |
(5) |
Here  K =
-(
K =
-( /3)
/3)
 is the dynamo
is the dynamo  -effect,
proportional to the kinetic helicity and
-effect,
proportional to the kinetic helicity and
 t
= (
t
= ( /3)
/3)
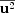 /3
is the turbulent magnetic diffusivity proportional to the kinetic energy
of the turbulence
[21].
/3
is the turbulent magnetic diffusivity proportional to the kinetic energy
of the turbulence
[21].
In the context of disk galaxies, the mean velocity
 is that
of differential rotation. This leads to the
is that
of differential rotation. This leads to the
 -effect, that of
shearing radial fields to produce toroidal fields,
while the
-effect, that of
shearing radial fields to produce toroidal fields,
while the  -effect is
crucial for regeneration of poloidal from toroidal fields.
A physical picture of the
-effect is
crucial for regeneration of poloidal from toroidal fields.
A physical picture of the
 -effect is as follows:
The interstellar medium is assumed
to become turbulent, due to for example the effect of supernovae randomly
going off in different regions. In a rotating, stratified
(in density and pressure) medium
like a disk galaxy, such turbulence becomes helical.
Helical turbulent motions of the gas
perpendicular to the disk draws out the toroidal field
into a loop which looks like a twisted
-effect is as follows:
The interstellar medium is assumed
to become turbulent, due to for example the effect of supernovae randomly
going off in different regions. In a rotating, stratified
(in density and pressure) medium
like a disk galaxy, such turbulence becomes helical.
Helical turbulent motions of the gas
perpendicular to the disk draws out the toroidal field
into a loop which looks like a twisted
 .
Such a twisted loop is connected to a current
which has a component parallel to the original toroidal
field. If the motions
have a non-zero net helicity, this
parallel component of the current adds up coherently.
A toroidal current then results from the toroidal field.
Hence, poloidal fields can be generated from toroidal ones.
(Of course microscopic diffusion is essential
to make permanent changes in the field). This closes the
toroidal-poloidal cycle and leads to exponential growth of the mean field.
The turbulent diffusion turns out to be also essential for allowing
changes in the mean field flux. The kinematic MFD equation 5.1,
gives a mathematical foundation to the above
picture. One finds exponentially growing solutions, of
the MFD equations provided a dimensionless dynamo number has magnitude
D = |
.
Such a twisted loop is connected to a current
which has a component parallel to the original toroidal
field. If the motions
have a non-zero net helicity, this
parallel component of the current adds up coherently.
A toroidal current then results from the toroidal field.
Hence, poloidal fields can be generated from toroidal ones.
(Of course microscopic diffusion is essential
to make permanent changes in the field). This closes the
toroidal-poloidal cycle and leads to exponential growth of the mean field.
The turbulent diffusion turns out to be also essential for allowing
changes in the mean field flux. The kinematic MFD equation 5.1,
gives a mathematical foundation to the above
picture. One finds exponentially growing solutions, of
the MFD equations provided a dimensionless dynamo number has magnitude
D = | 0
G h3
0
G h3
 t-2| >
Dcrit ~ 6
[11,
22],
a condition which can be satisfied in disk galaxies.
(Here h is the disk scale height and G the galactic shear,
t-2| >
Dcrit ~ 6
[11,
22],
a condition which can be satisfied in disk galaxies.
(Here h is the disk scale height and G the galactic shear,
 0 typical
value of
0 typical
value of  ,
and we have defined D to be positive). The mean field grows
typically on time-scales a few times the rotation time scales,
of order 3-10 × 108 yr.
,
and we have defined D to be positive). The mean field grows
typically on time-scales a few times the rotation time scales,
of order 3-10 × 108 yr.
This picture of the galactic dynamo faces several potential problems.
Firstly, while the mean field dynamo operates to generate
the large-scale field, the fluctuation dynamo is producing small-scale
fields at a much faster rate. Also the correlation time of
the turbulence measured by
u / l is not
likely to be small in turbulent flows. So the validity of FOSA is
questionable. Indeed, based on specific imposed (kinematic) flow
patterns it has been suggested that there is no simple relation between
/ l is not
likely to be small in turbulent flows. So the validity of FOSA is
questionable. Indeed, based on specific imposed (kinematic) flow
patterns it has been suggested that there is no simple relation between
 and helicity
of the flow; see
[23].
In order to clarify the existence of
and helicity
of the flow; see
[23].
In order to clarify the existence of
 -effect and turbulent
diffusion
as outlined above, and its Rm dependence,
even in the kinematic limit, we have recently measured
-effect and turbulent
diffusion
as outlined above, and its Rm dependence,
even in the kinematic limit, we have recently measured
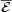 directly
in numerical simulations of isotropic, homogeneous, helical turbulence
[24].
These simulations reach up to
a modest Rm ~ 220. We find, somewhat surprisingly, that
for isotropic homogeneous turbulence the high conductivity results
obtained under FOSA are reasonably accurate up to the moderate
values of Rm that we have tested.
A possible reason for this might be that the
predictions of FOSA are very similar to a closure
called the minimal
directly
in numerical simulations of isotropic, homogeneous, helical turbulence
[24].
These simulations reach up to
a modest Rm ~ 220. We find, somewhat surprisingly, that
for isotropic homogeneous turbulence the high conductivity results
obtained under FOSA are reasonably accurate up to the moderate
values of Rm that we have tested.
A possible reason for this might be that the
predictions of FOSA are very similar to a closure
called the minimal
 approximation (MTA)
[27,
2]
where the approximation of neglecting nonlinear terms made in FOSA
is not done, but replaced by a closure hypothesis.
But MTA is also not well justified, although numerical
simulations (for Rm
approximation (MTA)
[27,
2]
where the approximation of neglecting nonlinear terms made in FOSA
is not done, but replaced by a closure hypothesis.
But MTA is also not well justified, although numerical
simulations (for Rm
 300)
support some aspects of this closure
[28].
Interestingly, this agreement of
300)
support some aspects of this closure
[28].
Interestingly, this agreement of
 and
and
 t
directly measured from the simulation, with that expected under FOSA, is
obtained even in the presence of a small-scale dynamo, where b is
growing exponentially. This suggests that the exponentially growing part
of the small-scale field does not make a contribution to the mean emf
t
directly measured from the simulation, with that expected under FOSA, is
obtained even in the presence of a small-scale dynamo, where b is
growing exponentially. This suggests that the exponentially growing part
of the small-scale field does not make a contribution to the mean emf
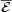 ,
correlated with the mean field
,
correlated with the mean field
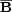 .
It is essential to extend these results to even higher values of
Rm,
but these preliminary results are quite encouraging.
.
It is essential to extend these results to even higher values of
Rm,
but these preliminary results are quite encouraging.
Another potential problem with the mean field dynamo paradigm
is that magnetic helicity conservation puts severe restrictions
on the strength of the
 -effect
[2].
The magnetic helicity associated with a field
B =
-effect
[2].
The magnetic helicity associated with a field
B =  ×
A is defined as Ht =
×
A is defined as Ht =
 A.B dV, where A is the vector potential
[21].
Note that this definition of
helicity is only gauge invariant (and hence meaningful) if the domain
of integration is periodic, infinite or has
a boundary where the normal component of the field vanishes.
Ht measures the linkages and twists in the magnetic field.
From the induction equation one can easily derive the
helicity conservation equation, dHt / dt = -2
A.B dV, where A is the vector potential
[21].
Note that this definition of
helicity is only gauge invariant (and hence meaningful) if the domain
of integration is periodic, infinite or has
a boundary where the normal component of the field vanishes.
Ht measures the linkages and twists in the magnetic field.
From the induction equation one can easily derive the
helicity conservation equation, dHt / dt = -2

 B
⋅ (
B
⋅ ( ×
B) dV. So in ideal MHD with
×
B) dV. So in ideal MHD with
 = 0,
magnetic helicity
is strictly conserved, but this does not guarantee
conservation of Ht in the limit
= 0,
magnetic helicity
is strictly conserved, but this does not guarantee
conservation of Ht in the limit

 0.
For example magnetic energy, whose Ohmic dissipation is governed by
(dEB / dt)Joule =
-
0.
For example magnetic energy, whose Ohmic dissipation is governed by
(dEB / dt)Joule =
- (4
(4 / c2)
/ c2)
 J2 dV,
can be dissipated at finite rates even in the limit
J2 dV,
can be dissipated at finite rates even in the limit

 0,
because small enough scales develop in the field (current sheets)
where the current density increases with decreasing
0,
because small enough scales develop in the field (current sheets)
where the current density increases with decreasing
 as
as

 -1/2
as
-1/2
as 
 0.
Nevertheless, since helicity dissipation rate has a milder dependence on
the current density (its rate being proportional to J ⋅
B and not J2), in many astrophysical conditions
where Rm is
large (
0.
Nevertheless, since helicity dissipation rate has a milder dependence on
the current density (its rate being proportional to J ⋅
B and not J2), in many astrophysical conditions
where Rm is
large ( small), the magnetic helicity Ht, is almost
independent
of time, even when the magnetic energy is dissipated at finite rates.
small), the magnetic helicity Ht, is almost
independent
of time, even when the magnetic energy is dissipated at finite rates.
The operation of any mean-field dynamo automatically leads to
the growth of linkages between the toroidal and poloidal mean fields
and hence a mean field helicity. In order to satisfy total
helicity conservation this implies that there must be equal and oppositely
signed helicity being generated in the fluctuating field.
What leads to this helicity transfer between scales?
To understand this, we need to split the helicity conservation
equation into evolution equations of the
sub-helicities associated with the mean field, say
 t =
t =

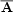 ⋅
⋅
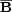 dV and the
fluctuating field ht =
dV and the
fluctuating field ht =
 a ⋅ b dV . The evolution equations for
a ⋅ b dV . The evolution equations for
 t and
ht are
[2]
t and
ht are
[2]
 |
Here, we have assumed that the surface terms can be taken to
vanish (we will return to this issue below).
We see that the turbulent emf
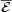 transfers helicity between large and small scales;
it puts equal and opposite amounts of helicity into
the mean field and the small-scale field, conserving
the total helicity Ht =
transfers helicity between large and small scales;
it puts equal and opposite amounts of helicity into
the mean field and the small-scale field, conserving
the total helicity Ht =
 t +
ht. Note that in the limit when the fluctuating field
has reached a stationary state one has dht / dt
t +
ht. Note that in the limit when the fluctuating field
has reached a stationary state one has dht / dt
 0
and
0
and 
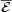 ⋅
⋅
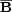 dV =
-2
dV =
-2 
 (4
(4 / c) j
⋅ b dV which tends to zero as
/ c) j
⋅ b dV which tends to zero as

 0
for any reasonable spectrum of small scale current helicity.
Therefore, the component of the turbulent electromotive force
along the mean field is catastrophically quenched in the sense that
it tends to zero as
0
for any reasonable spectrum of small scale current helicity.
Therefore, the component of the turbulent electromotive force
along the mean field is catastrophically quenched in the sense that
it tends to zero as

 0, or for large
Rm,
a feature also borne out in periodic box simulations
[19,
25].
0, or for large
Rm,
a feature also borne out in periodic box simulations
[19,
25].
To make the above integral constraint into a local constraint requires one to be able to define a gauge invariant helicity density for at least the random small-scale field. Such a definition has indeed been given, using the Gauss linking formula for helicity [26]. In physical terms, the magnetic helicity density h of a random small scale field (in contrast to the total helicity ht), is the density of correlated links of the field. This notion can be made precise and a local conservation law can be derived (see [26] for details) for the helicity density h,
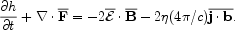 |
(5) |
where 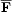 gives a
flux density of helicity.
(For a weakly inhomogeneous system, h is approximately
gives a
flux density of helicity.
(For a weakly inhomogeneous system, h is approximately
 in the Coulomb gauge.) In the presence of helicity fluxes, we have
in the stationary limit,
in the Coulomb gauge.) In the presence of helicity fluxes, we have
in the stationary limit,
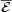 ⋅
⋅
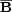 =
-(1/2)
=
-(1/2) ⋅
⋅
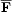 -
-
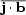 ,
and therefore
,
and therefore 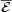 ⋅
⋅
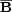 need not be
catastrophically quenched.
Large scale dynamos then seem to need helicity fluxes to work efficiently
[29,
30,
31].
need not be
catastrophically quenched.
Large scale dynamos then seem to need helicity fluxes to work efficiently
[29,
30,
31].
This conclusion can be understood more physically as follows:
As the large-scale mean field grows the turbulent emf
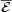 is transferring
helicity between the small and large scale fields.
The large scale helicity is in the links of the mean poloidal
and toroidal fields, while the small scale helicity is
in what can be described as "twist" helicity of the
small-scale field. Lorentz forces associated with the
"twisted" small-scale field would like to untwist the field.
This would lead to an effective magnetic
is transferring
helicity between the small and large scale fields.
The large scale helicity is in the links of the mean poloidal
and toroidal fields, while the small scale helicity is
in what can be described as "twist" helicity of the
small-scale field. Lorentz forces associated with the
"twisted" small-scale field would like to untwist the field.
This would lead to an effective magnetic
 -effect
which opposes the kinetic
-effect
which opposes the kinetic  produced by the helical turbulence (see below). The cancellation
of the total
produced by the helical turbulence (see below). The cancellation
of the total  -effect is
what leads to the catastrophic quenching of the dynamo. This quenching can
be avoided if there is some way of transferring the twists
in the small scale field out of the region of dynamo action,
that is if there are helicity fluxes out of the system.
-effect is
what leads to the catastrophic quenching of the dynamo. This quenching can
be avoided if there is some way of transferring the twists
in the small scale field out of the region of dynamo action,
that is if there are helicity fluxes out of the system.
Blackman and Field (in
[29])
first suggested that the losses of the
small-scale magnetic helicity through the boundaries of the dynamo
region can be essential for mean-field dynamo action. Such a helicity
flux can result from the anisotropy of the turbulence combined with
large-scale velocity shear or the non-uniformity of the
 -effect
[29].
Another type of helcity flux is simply advection
of the small scale field and its associated helicity out of the
system, with
-effect
[29].
Another type of helcity flux is simply advection
of the small scale field and its associated helicity out of the
system, with
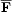 = h
= h
 [30].
This effect naturally arises in spiral galaxies where some of the gas
is heated by supernova explosions producing a hot phase that
leaves the galactic disc, dragging along the small-scale part of
the interstellar magnetic field.
[30].
This effect naturally arises in spiral galaxies where some of the gas
is heated by supernova explosions producing a hot phase that
leaves the galactic disc, dragging along the small-scale part of
the interstellar magnetic field.
In order to examine the effect of helicity fluxes in more detail,
one also needs to fold in a model of how the dynamo
co-efficients get altered due to Lorentz forces.
Closure models either using the EDQNM closure
or the MTA or quasi-linear theory,
suggest that the turbulent emf gets re-normalized, with
 =
=
 K +
K +
 m, where
m, where
 m =
(
m =
( /3) <
b.
/3) <
b. ×
b> / (4
×
b> / (4
 ),
is proportional to the small-scale current helicity
and is the magnetic alpha effect mentioned above
[2,
27,
32].
The turbulent diffusion
),
is proportional to the small-scale current helicity
and is the magnetic alpha effect mentioned above
[2,
27,
32].
The turbulent diffusion
 t
is left unchanged to the lowest order, although to the next
order there arises a non-linear hyperdiffusive correction
[16].
Some authors have argued against an
t
is left unchanged to the lowest order, although to the next
order there arises a non-linear hyperdiffusive correction
[16].
Some authors have argued against an
 m contribution,
and suggest instead that the
m contribution,
and suggest instead that the
 -effect
can be expressed exclusively in terms of
the velocity field, albeit one which is a solution
of the full momentum equation including the Lorentz force
[33].
To clarify this issue, we have studied the nonlinear
-effect
can be expressed exclusively in terms of
the velocity field, albeit one which is a solution
of the full momentum equation including the Lorentz force
[33].
To clarify this issue, we have studied the nonlinear
 -effect in the limit of
small Rm,Re << 1 using FOSA
applied to both induction and momentum equations
[34].
We show explicitly in this limit that one can express
-effect in the limit of
small Rm,Re << 1 using FOSA
applied to both induction and momentum equations
[34].
We show explicitly in this limit that one can express
 completely
in terms of the helical properties of the velocity field
as in traditional FOSA, or, alternatively, as the sum of two terms,
a so-called kinetic
completely
in terms of the helical properties of the velocity field
as in traditional FOSA, or, alternatively, as the sum of two terms,
a so-called kinetic  -effect
and an oppositely signed term proportional to the
helical part of the small scale magnetic field,
akin to the above closures.
-effect
and an oppositely signed term proportional to the
helical part of the small scale magnetic field,
akin to the above closures.
Adopting  =
=
 K +
K +
 m as above, one
can now look for a combined solution
to the helicity conservation equation (5.3), and the mean-field
dynamo equation
[2,
35],
after relating the current helicity arising in
m as above, one
can now look for a combined solution
to the helicity conservation equation (5.3), and the mean-field
dynamo equation
[2,
35],
after relating the current helicity arising in
 m to the
magnetic helicity density h.
The effect of the advective flux in resolving the quenching of
the dynamo was worked out in detail in Ref
[30].
In the absence of an advective flux, the
initial growth of magnetic field is
catastrophically quenched and the large-scale magnetic field decreases
at about the same rate as it grew.
The initial growth occurs while the current helicity builds up to
cancel the kinetic
m to the
magnetic helicity density h.
The effect of the advective flux in resolving the quenching of
the dynamo was worked out in detail in Ref
[30].
In the absence of an advective flux, the
initial growth of magnetic field is
catastrophically quenched and the large-scale magnetic field decreases
at about the same rate as it grew.
The initial growth occurs while the current helicity builds up to
cancel the kinetic  -effect.
However, even a modest advective flux compensates the
catastrophic quenching of the dynamo and the mean field
stays steady at about 10% of the equipartition value.
(Excessive advection, however, hinders the dynamo as it
removes the mean field from the dynamo active region).
The vertical advection of magnetic helicity by galactic fountain flow
can therefore resolve in a straightforward fashion the
catastrophic quenching of nonlinear mean-field galactic dynamos.
Further, advection of small-scale magnetic fields
may help the mean-field dynamo action in other ways.
For example, there is a concern that the back-reaction of Lorentz forces
due to the rapidly growing small-scale field could quench turbulent
transport processes, simply by suppressing the required Lagrangian chaos.
In this case their advection out of the galaxy
will still allow the dynamo to operate efficiently.
-effect.
However, even a modest advective flux compensates the
catastrophic quenching of the dynamo and the mean field
stays steady at about 10% of the equipartition value.
(Excessive advection, however, hinders the dynamo as it
removes the mean field from the dynamo active region).
The vertical advection of magnetic helicity by galactic fountain flow
can therefore resolve in a straightforward fashion the
catastrophic quenching of nonlinear mean-field galactic dynamos.
Further, advection of small-scale magnetic fields
may help the mean-field dynamo action in other ways.
For example, there is a concern that the back-reaction of Lorentz forces
due to the rapidly growing small-scale field could quench turbulent
transport processes, simply by suppressing the required Lagrangian chaos.
In this case their advection out of the galaxy
will still allow the dynamo to operate efficiently.
We have emphasized so far the role of helicity for the dynamo generation of large-scale fields. Intriguingly, several recent simulations show that the generation of large-scale fields may arise even in non-helical turbulence in the presence of strong enough shear [36]. It is at present an important open question as the exact cause of such large-scale field generation.