I conclude with an attempt to resolve an old dispute about the axis ratio of the local velocity ellipsoid expected from scattering by giant molecular clouds. Though a side issue to the main thread of this brief review, it has provided an additional, apparently compelling, argument in favor of spirals as short-lived transients that now turns out to have no weight.
Lacey (1984) and Binney & Lacey (1988) calculated the separate growth of the in-plane and vertical components, concluding that cloud scattering should cause the vertical component to be intermediate between the radial and azimuthal components. Their result seems physically plausible on energy equipartition grounds: scattering by massive clouds redirects the peculiar motions of stars through random angles, and therefore isotropizes the motions as far as is possible.
However, this is not what is observed. The second moments of the
velocity distribution of solar neighborhood stars in the three
orthogonal directions are unequal
(Wielen 1977;
Dehnen & Binney
1998;
Nordström et
al. 2004).
The radial component,
u, is the
largest, the azimuthal component,
v,
intermediate and the vertical component,
w, is the
smallest, and this remains true
for all groups when the stars are subdivided according to the best
estimates of their ages. The ratio of the two in-plane components is
set by the epicyclic motions, and is in reasonable agreement with
theoretical expectations (e.g.
Dehnen & Binney
1998).
Some estimates of the velocity ellipsoid shape in external galaxies are
beginning to be made
(Gerssen et al.
1997,
2000;
Ciardullo et al.
2004;
Westfall et al., these proceedings).
Carlberg (1987) and Jenkins & Binney (1990) therefore developed the plausible argument that spirals drive up the in-plane components more rapidly than scattering is able to redirect those motions into the vertical direction, thereby accounting for the observed axis ratios of the velocity ellipsoid. Their argument appeared to offer strong support for the transient spiral picture, but this particular line of argument now seems to be incorrect.
The conclusion by Lacey (1984) and Binney & Lacey (1988) that cloud scattering would lead to the vertical dispersion being intermediate between the radial and azimuthal dispersions was challenged by Ida, Kokuba & Makino (1993). These authors claimed that cloud scattering alone would lead to the vertical component being the smallest, as confirmed in numerical simulations (Shiidsuke & Ida 1999). Ida et al. ( 1993) also show how the axis ratio depends on the local slope of the rotation curve. Their two papers have attracted little attention, largely because they are hard to follow, and their physical explanation for their different conclusion is rather enigmatic. Accordingly, I here describe some idealized simulations to determine what should be the shape of the velocity ellipsoid due to scattering by randomly distributed, co-orbiting mass clumps.
I wish to study the motion of collisionless stars in an axisymmetric disk potential that is smooth except for the presence of a collection of non-interacting scattering masses. I treat the stars as test particles moving in an axisymmetric, vertically stratified, potential and integrate their motion subject to perturbations from a collection of co-moving heavy particles. Following Wisdom & Tremaine (1988) for a Keplerian disk and Toomre & Kalnajs (1991) for a constant-velocity disk, I consider a small orbiting patch of the disk, with periodic boundary conditions and adjacent radial boxes sliding past the main box at the local shear rate. These authors describe the set-up of sheared sheet simulations more fully.
I assume a flat rotation curve for the in-plane accelerations, while
the vertical density profile has the form
(z) =
0
sech2(z / 2z0)
for the isothermal sheet
(Spitzer 1942;
BTII). The heavy particles, which contain 20% of the local surface density,
affect the vertical balance and I reduce the nominal surface mass
density that gives rise to the fixed potential by the mass in the
heavies, which are distributed in a thinner layer. The heavy
particles all start with random motions that are 5% of those of the
test particles, with a corresponding reduction in the thickness of the
layer of heavies. I have verified that the final shape of the
velocity ellipsoid is insensitive to the fraction of mass in the heavy
particles or their velocity dispersions.
The initial in-plane velocities of the test particles are set such
that, were the disk self-gravitating, Toomre's Q = 1 and the epicycle
approximation requires
u =
21/2
v. There can be
no asymmetric drift in the sheared sheet, since the symmetry of the
equations does not determine the direction to the center of the
galaxy. The initial vertical positions and speeds of all test
particles are set to ensure vertical balance. The principal parameter
I vary is the initial vertical velocity dispersion of the test
particles. The scale height is related to the dispersion as
z0 =
w2 /
(2
G
). As the
vertical motions of the test
particles rise, I make corresponding adjustments to the scale height
of the potential, although the final shape of the velocity ellipsoid
is little affected by turning this refinement on or off.
I adopt the usual Plummer potential for each heavy particle, with a softening length of 0.01R0, where R0 is our fourth the radial extent of the sheared patch under study. The maximum range of the perturbing forces from the heavy particles in the adopted shearing box arrangement that can be conveniently handled is the radial extent of the box. The position of every heavy particle is duplicated in the surrounding boxes and the perturbing forces from all the heavy particles and their images separately affect the motion of the test particles in the main box.
As the integration proceeds, the shape of the velocity ellipsoid of
the test particles evolves towards a steady value, while the total
magnitude of the velocity dispersion rises slowly. I find that
irrespective of whether I begin with a round or strongly flattened
velocity ellipsoid, it quickly evolves to a shape in which the
vertical dispersion is slightly smaller than the azimuthal dispersion.
The final ellipsiod shape is always
u :
v :
w
1 : 0.71 : 0.62,
confirming the prediction by Ida and coworkers, and in disagreement with
the results by Lacey and Binney & Lacey. The physically plausible
energy equipartition argument must also be misleading.
It seemed possible that this prediction fails in a thin disk because
the distribution of scatterers is not uniform. As with any scattering
process in 3-D, the
ln
term implies
that distant encounters
dominate. But distant scatterers in the flattened geometry of a disk
are not isotropically distributed, and scattering by distant clouds
must predominantly affect the in-plane star velocities, and couple
much less strongly to the vertical component.
In order to test this idea, I experimented with excluding the
influence of the disturbance forces from all heavy particles more
distant than dmax. Figure 1
shows the equilibrium
ratio w /
u plotted as
a function of dmax. The
ratio settles to something close to the energy equipartition
prediction when none but the closest heavy scatterers perturb the
stars, but as I increase the range of scattering in separate
experiments, the final ellipsoid gradually becomes flatter and
approaches Ida's result for no cut off.
 |
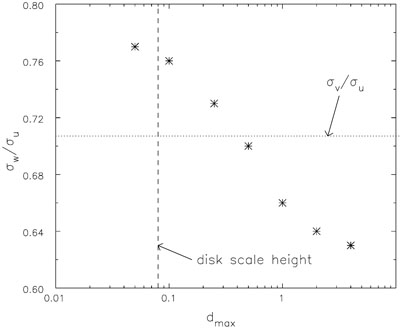Figure 1. The effect on the equilibrium axis ratio of the velocity ellipsoid of limiting the range of the perturbation forces from the heavy particles. |
This test therefore clearly supports the idea that the anisotropic distribution of the scatterers determines the equilibrium shape of the velocity ellipsoid. Previous studies (Spitzer & Schwarschild 1953; Lacey 1984; Binney & Lacey 1988) assumed that scattering is dominated by impact parameters that are small compared to both the epicycle radius and the disk thickness and peculiar velocities were the most important.
Thus the shape of the local velocity ellipsoid (e.g. Nordström et al. 2004) is apparently consistent with cloud scattering, and its origin does not require concurrent spiral arm scattering, as seemed attractive. However, the data do not imply that spirals are unimportant: there are hints of some evolution of the velocity ellipsoid shape that may demand a compound origin, and the magnitude of the random speeds of the oldest stars may still require an additional source of scattering (e.g. Lacey 1991).
Acknowledgments. I thank Scott Tremaine for insisting that I should better understand the reason for the shape of the local velocity ellipsoid, and for some helpful correspondence. I thank Cedric Lacey, Ray Carlberg, Victor Debattista and especially James Binney for perceptive comments on the manuscript. This work was supported by grants AST-0507323 from the NSF and NNG05GC29G from NASA.