Barba et al. (2009) examined the giant star-forming region NGC 604 in M33 with NICMOS, finding mostly unclustered stars. Maíz-Apellániz (2001) categorized star formation regions according to three types: compact clusters with weak halos, measuring 50 × 50 pc2, compact clusters with strong halos measuring 100 × 100 pc2, and hierarchical, but no clusters, called "Scaled OB Associations" (SOBAs), measuring 100 × 100 pc2. Why do stars form in clusters some of the time but not always?
The occurrence of bound clusters in star forming regions could depend on many factors, but the pressure of the region relative to the average pressure should be important. Higher pressure regions should produce proportionally more clusters. Recall, that Elias, Alfaro & Cabrera-caño (2009) found a higher clustering fraction for the high-pressure Orion region compared to the low-pressure Sco-Cen region. One reason for a possible pressure dependence was discussed in Elmegreen (2008) and is reviewed here.
Turbulence produces a log-normal density probability distribution
function
(Vazquez-Semadeni
1994,
Price et
al. 2010),
and this corresponds to a log-normal
cumulative mass fraction fM (>
), which is
the fraction of the gas mass with a density larger than the value
. This is a
monotonically decreasing function of
. If the
densest clumps have a density
c,
and the star formation rate per unit volume
is the dynamical rate for all densities with an efficiency (star-to-gas
mass fraction) that depends on density, i.e., SFR =
()
(G
)1/2,
then the mass fraction of the densest clumps inside a region of average
density is
 |
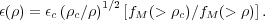(7.1) |
This function ()
increases with
for
intermediate to high density. If stars form
in the densest clumps with local efficiency
c (~
0.3), then
() is the
efficiency of star formation,
i.e., the mass fraction going into stars for each average density.
Bound clusters form where the efficiency is highest, and this is where
the average density is highest. If we consider the density where
() exceeds a
certain minimum value for a bound cluster, then most star formation at
this density or larger ends up in bound clusters.
Note that the observation of cluster boundedness appears to be independent of cluster mass and therefore independent of the presence of OB stars in the cluster. Bound clusters with highly disruptive OB stars form in dense cloud cores, just like clusters without these stars. The efficiency of star formation is therefore not related in any obvious way to the presence or lack of disruptive stars. The implication is that essentially all of the stars in a cluster form before OB-star disruption occurs. Perhaps the highly embedded nature of OB star formation, in ultracompact HII regions, for example, shields the rest of the cloud core from disruption for a long enough time to allow the lower mass cores to collapse into stars.
The pressure dependence for cluster boundedness arises in the theory of
Elmegreen (2008)
because at a fixed density for star formation, the
slope of the fM(>
) curve
decreases for higher average
density (the log-normal shifts to higher density), and the slope also
decreases for higher Mach number because the log-normal gets broader.
With a shallower slope at the density of star formation, the density
where ()
exceeds the limit for bound cluster formation
decreases, and the fraction of the mass exceeding this density
increases. Thus forming a bound cluster happens at a lower density
relative to the threshold for star formation when the pressure is high.
A higher fraction of the gas then goes into bound clusters. The
qualitative nature of this conclusion is independent of the details of
the density pdf.
This discussion of cluster formation in a hierarchical medium assumes that the gas structure is already in place when star formation begins, and then the densest clumps, which are initially clustered together, form stars. The discussion can be made more dynamical if we consider that the denser regions fragment faster. This is what happens during a collapse simulation: the dense regions make more subcondensations and the low density regions collapse on to the dense regions. The result is a clustering of dense sub-condensations and a hierarchical clustering of stars.